Question

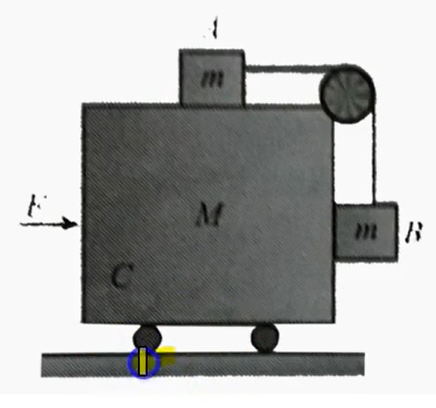
Consider the situation shown in figure. The horizontal surface below the bigger block is smooth. The coefficient of friction between the blocks is ${\displaystyle \mu }$. Find the minimum and the maximum force F that can be applied in order to keep the smaller block at rest with respect to the bigger block.

Explanation

If no force is applied, the block A will slip on C towards right and the block B will move downward. Suppose the minimum force needed to prevent sliping is F. Taking A+B+C as the system, the obly exterN/Al horizontal force on the system is F. Hence the acceleratioinof the system is
` a=F/(M+2m)`..........i
Now take the block a as the system. The forces on A are.
,

i. tension t by the string towards right,
ii. friction fi by the block C towards left,
iii. weight mg downward and
normal force N upward
For veticla equilibrium N=mg
As the minimum force neede dto prevent slipping is appied, the fricton is limiting. Thus,
f=mu N=mu mg`
As the block moves towards right with an acceleration a
`T-f=ma`
or `T-mu mg=ma`.........ii
Now take the block B as the system. The forces are,
i. Tension T upward
ii. weight mg downward
iii. normal force N towards right and
friction f upward
As the block moves towards right with an acceleration a,
`N'=ma`
As the friction is limiting `f'=mu N'=mu ma`
For vertical equilibrium
`T+f'=mg`
or `T+mu ma =mg` ..........iii
ElimiN/Ating T from ii. and iii
`a_(min)=(1-mu)/(1+mu) g`.
When a large force is appied the block A slips on C towards left and the block B slips on C in the upward directin. The friction on A is towards right and that on B is downwards. Solving as above, the acceleration in this case is
`a_(max)=(1+mu)/(1-mu)g`
Thus, a lies between `(1-mu)/(1+mu)g and (1+mu)/(1-mu)g`
from the force F should be between
` (1-mu)/(1+mu)(M+2m) g and (1+mu)/(1-mu)(M+2m)g`.