An aeroplane has to go from a point A to another point B, away due east of north. Wind is blowing due north at a speed of The air-speed of the plane is (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.Solution in Tamil
The correct Answer is:A, B
IN resultant direction , the plane reaches the point B.
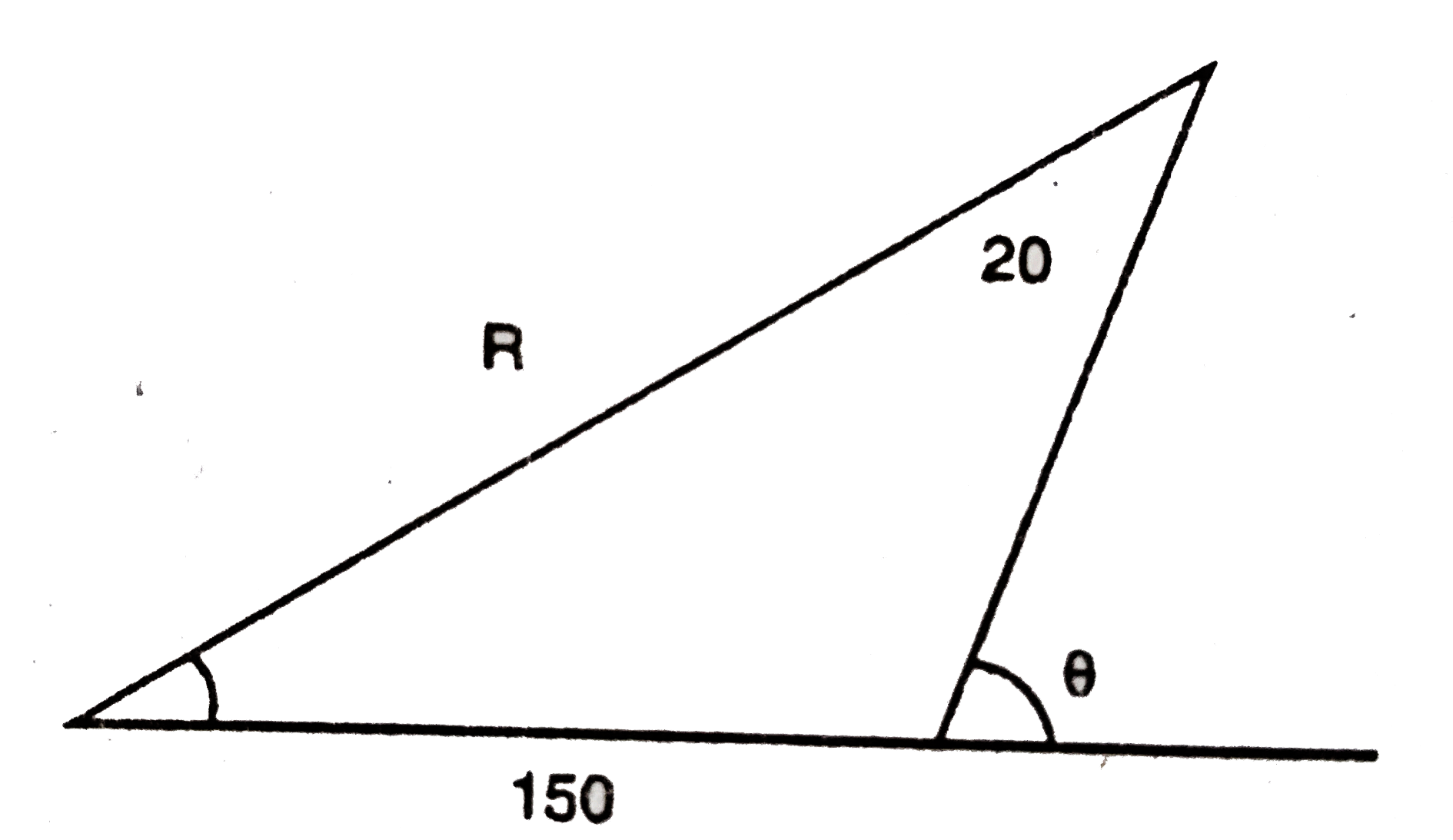
In according to sine formula
a The direction is east of the line AB.
b.
R=sqrt(150+20+2(150)20 cos (33^0 48')) = sqrt(27886) = 167 m/s time = S/v = 500000/167 = 2994 sec = 49.0 ~~ 50 min.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
Consider the motion of the tip of the minute hand of a clock. In one hour
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200 km//h. The air speed of plane is 500 km//h. (a) Find the direction in which the pilot should head the plane to reach the point Q. (b) Find the time taken by the plane to go from P to Q.
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
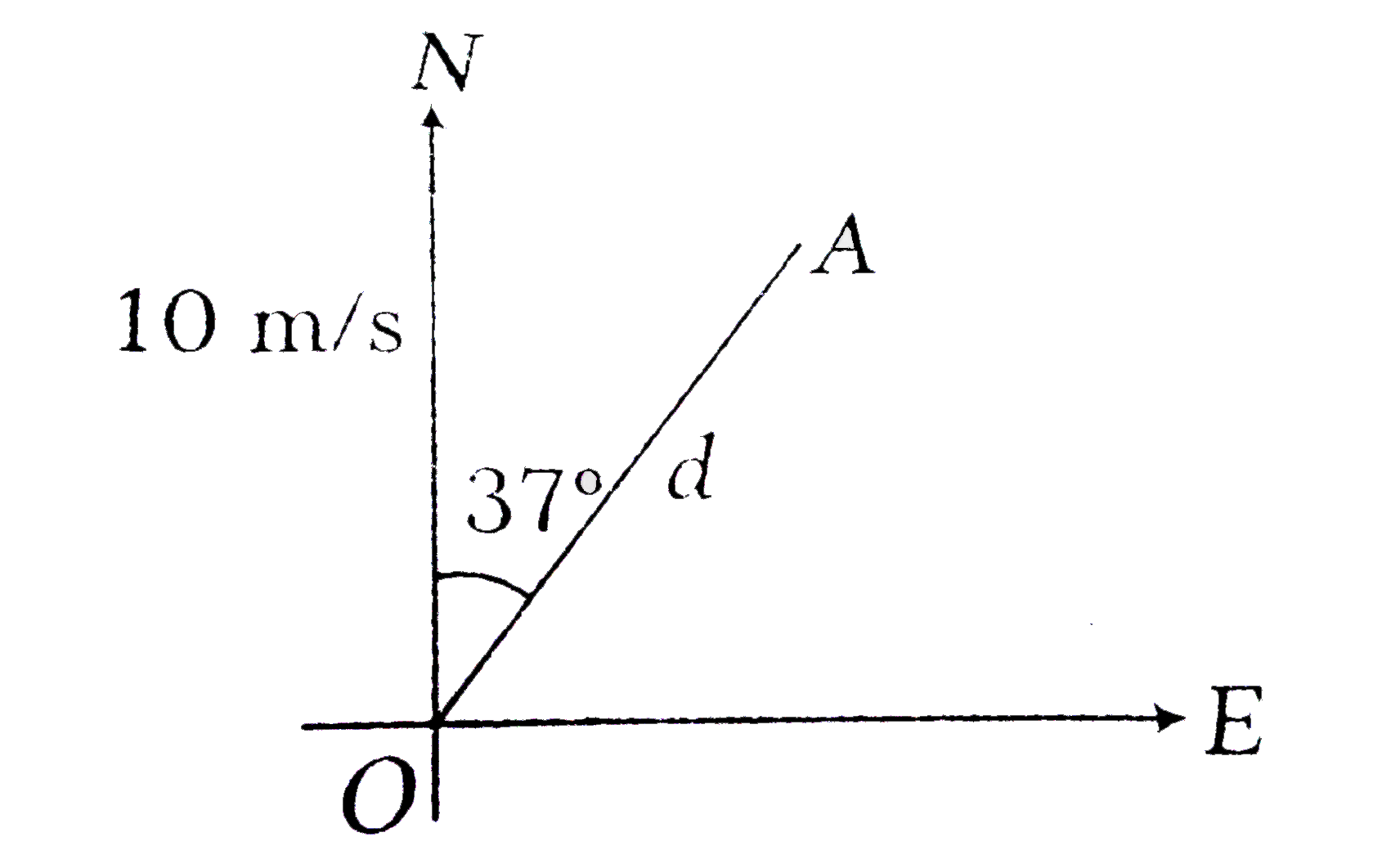
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ east of north. A wind is blowing due north at a speed of 20m/s. The air speed of the plane is v. (a) Find the direction in whihc the pilot should head the plane to reach the point A. (b) Find the time taken by the plane to go from O to A.
View SolutionA plane is to fly due north. The speed of the plane relative to the air is 200 km/h, and the wind is blowing from west to east at 90 km/h.
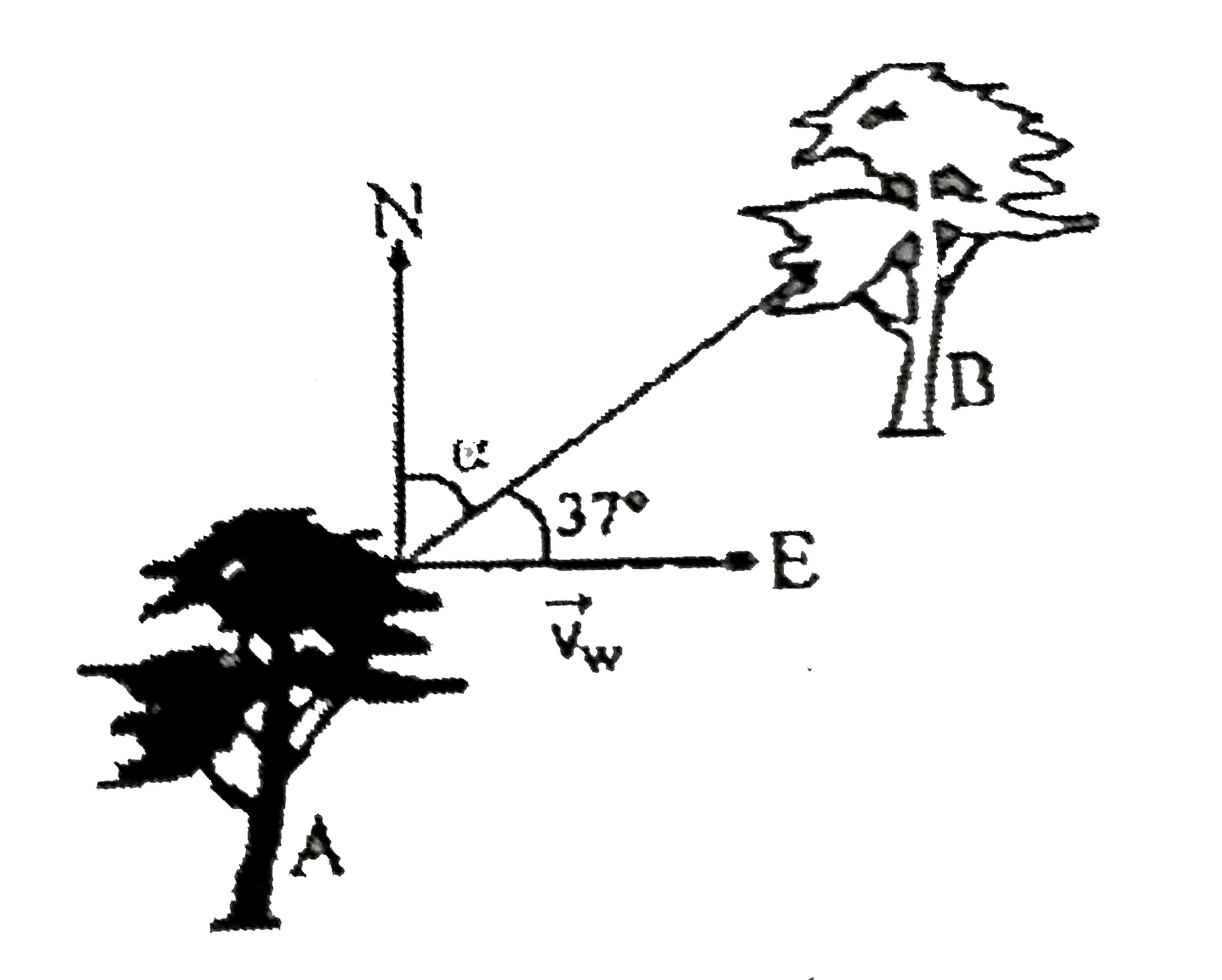
View SolutionWind is blowing in the east direction with a speed of 2m/s. A,. bird wishes to travel from tree A to tree B. Tree B is 100 m · away from A in a direction 37∘ north of east the velocity of ·bird in still air is 4 m/s.
( a) Find the direction in which bird should fly so that it can reach from A to B directly.
(b) Find the actual velocity of the bird during the flight.
(c) Find the time taken by the bird to reach B.
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionA plane moves in windy weather due east while the pilot the plane somewhat south of east. The wind is blowing at 50 km/h directed 30∘ east of north, while the palne moves at 200 km/h relative to the wind . What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the palne ?
View Solutionएक हवाई जहाज को स्थान A से स्थान B तक जाना है । B की दुरी A से 500 km और AB की दिशा उत्तर से 30∘ पूर्व की और है । उत्तर की और 20 m/s की चाल से हवा बह रही है हवा के सापेक्ष जहाज की चाल 150 m/स है । (a) पायलट को हवाई जहाज किस दिशा में (हवा के सापेक्ष ) उड़ाना चाहिए ताकि वह स्थान A पर पहुँचा जाए । (b) स्थान A से स्थान B तक पहुँचने में जहाज को कितना समय लगेगा ?
View SolutionA plane moves due east while the pilot points the plane somewhat south of east, toward a steady wind that blows to the northeast. The plane has velocity vecv_(PW) relative to the wind, with an airspeed (speed relative to the wind) of 215 km/h, directed at angle theta south of east. The wind has velocity vecv_(WG) is relative to the ground with speed 65.0 km/h, directed 20.0^@ cast of north. What is the magnitude of the velocity vec_(PG) of the plane relative to the ground, and what is theta ?
View SolutionAfter flying for 18 min in a wind blowing 42 km/h at an angle of 20∘ south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
View SolutionA light plane attains an airspeed of 500 km/h. The pilot sets out for a destination 900 km due north but discovers that the plane must be headed 20.0∘ east of due north to fly there directly. The plane arrives in 2.00 h. What were the (a) magnitude and (b) direction of the wind velocity?
View SolutionThe captain of a plane wishes to proceed due west. The cruising speed of the plane is 245 m/s relative to the air. A weather report indicates that a 38.0 m/s wind is blowing from the south to the north. In what direction, measured with respect to due west, should the pilot head the plane relative to the air?
View SolutionAn airplane pilot wants to fly from city A to city B which is 1000 km due north of city A. The speed of the plane in still air is 500 km/hr. The pilot neglects the effect of the wind and directs his plane due north and 2 hours later find himself 300 km due north-east of city B. The wind velocity is
View Solution
