An aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
The correct Answer is:A, B, D
To solve the problem, we need to break it down into two parts as specified in the question.
Part (a): Find the direction in which the pilot should head the plane to reach point Q.
1. Identify the given information:
- Distance from P to Q (D) = 1000 km (due North)
- Wind speed (Vw) = 200 km/h (due East)
- Air speed of the plane (Va) = 500 km/h
2. Set up the components of the velocities:
- The plane's velocity can be broken down into two components:
- Northward component: Vacos(θ)
- Eastward component: Vasin(θ)
3. Condition for reaching point Q:
- To ensure the plane reaches point Q directly north, the eastward component of the plane's velocity must cancel out the wind's velocity:
Vasin(θ)=Vw
Substituting the values:
500sin(θ)=200
sin(θ)=200500=25
4. Calculate the angle θ:
- To find θ, we take the inverse sine:
θ=sin−1(25)
5. Find the cosine of the angle:
- Using the Pythagorean identity:
cos(θ)=√1−sin2(θ)=√1−(25)2=√1−425=√2125=√215
6. Determine the heading direction:
- The pilot should head the plane at an angle θ north of west, where θ=sin−1(25).
Part (b): Find the time taken by the plane to go from P to Q.
1. Calculate the northward component of the plane's velocity:
Vacos(θ)=500cos(θ)=500⋅√215=100√21 km/h
2. Use the formula for time:
Time(T)=DistanceVelocity=DVacos(θ)
Substituting the values:
T=1000100√21=10√21 hours
Final Answers:
- (a) The pilot should head the plane at an angle θ=sin−1(25) north of west.
- (b) The time taken by the plane to go from P to Q is 10√21 hours.
- Distance from P to Q (D) = 1000 km (due North)
- Wind speed (Vw) = 200 km/h (due East)
- Air speed of the plane (Va) = 500 km/h
- The plane's velocity can be broken down into two components:
- Northward component: Vacos(θ)
- Eastward component: Vasin(θ)
- To ensure the plane reaches point Q directly north, the eastward component of the plane's velocity must cancel out the wind's velocity:
Vasin(θ)=Vw
Substituting the values:
500sin(θ)=200
sin(θ)=200500=25
- To find θ, we take the inverse sine:
θ=sin−1(25)
- Using the Pythagorean identity:
cos(θ)=√1−sin2(θ)=√1−(25)2=√1−425=√2125=√215
- The pilot should head the plane at an angle θ north of west, where θ=sin−1(25).
Vacos(θ)=500cos(θ)=500⋅√215=100√21 km/h
Time(T)=DistanceVelocity=DVacos(θ)
Substituting the values:
T=1000100√21=10√21 hours
- (a) The pilot should head the plane at an angle θ=sin−1(25) north of west.
- (b) The time taken by the plane to go from P to Q is 10√21 hours.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
An aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The steering-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go fram A to B.
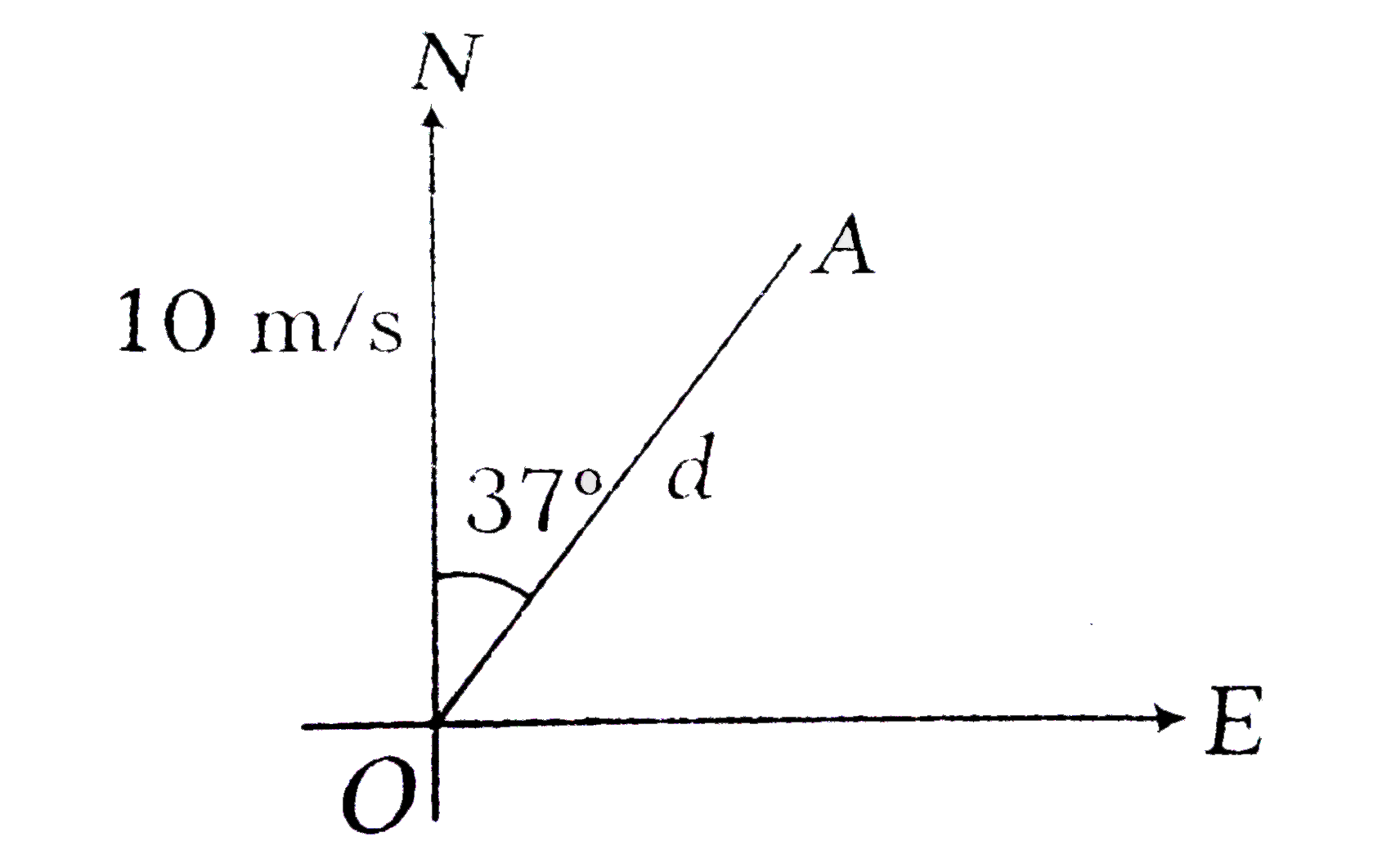
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ east of north. A wind is blowing due north at a speed of 20m/s. The air speed of the plane is v. (a) Find the direction in whihc the pilot should head the plane to reach the point A. (b) Find the time taken by the plane to go from O to A.
View Solution
Knowledge Check
A person goes from one point to another point with a speed of 5km/h and comes back to starting point with a speed of 3 km/h. Find the average speed for the whole journey.
A4.5 km/hB4 km/hC4.25 km/hD3.75 km/hA ship is travelling due east at a speed of 15km/h. Find the speed of a boat heading 30∘ east of north if it appears always due north from the ship.
A30km/hB15√32km/hC10√3km/hD20km/hA person P is at X and another person Q is atY. The distance between X and Y is 100 km. The speed of P is 20 km/h. While the speed of Q is 60 km/h?
If they first time meet at point Z somewhere between X and Y then the distance between X and Z is :A20 kmB40 kmC25 kmD30 km
An aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionA plane is to fly due north. The speed of the plane relative to the air is 200 km/h, and the wind is blowing from west to east at 90 km/h.
View SolutionA plane is travelling eastward at a speed of 500kmh−1. But a 90kmh−1 wind is blowing southward. What is the direction and speed of the plane relative to the ground ?
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
View SolutionAn aeroplane fles a straight path from town (A) to town B,500km way . Town (B) is due East ot town (A) and a strong with blows from South to North at 1 300 km//h.Tfthela≠s air speed is 900km/h. Which of following statements is true ?
View Solution
