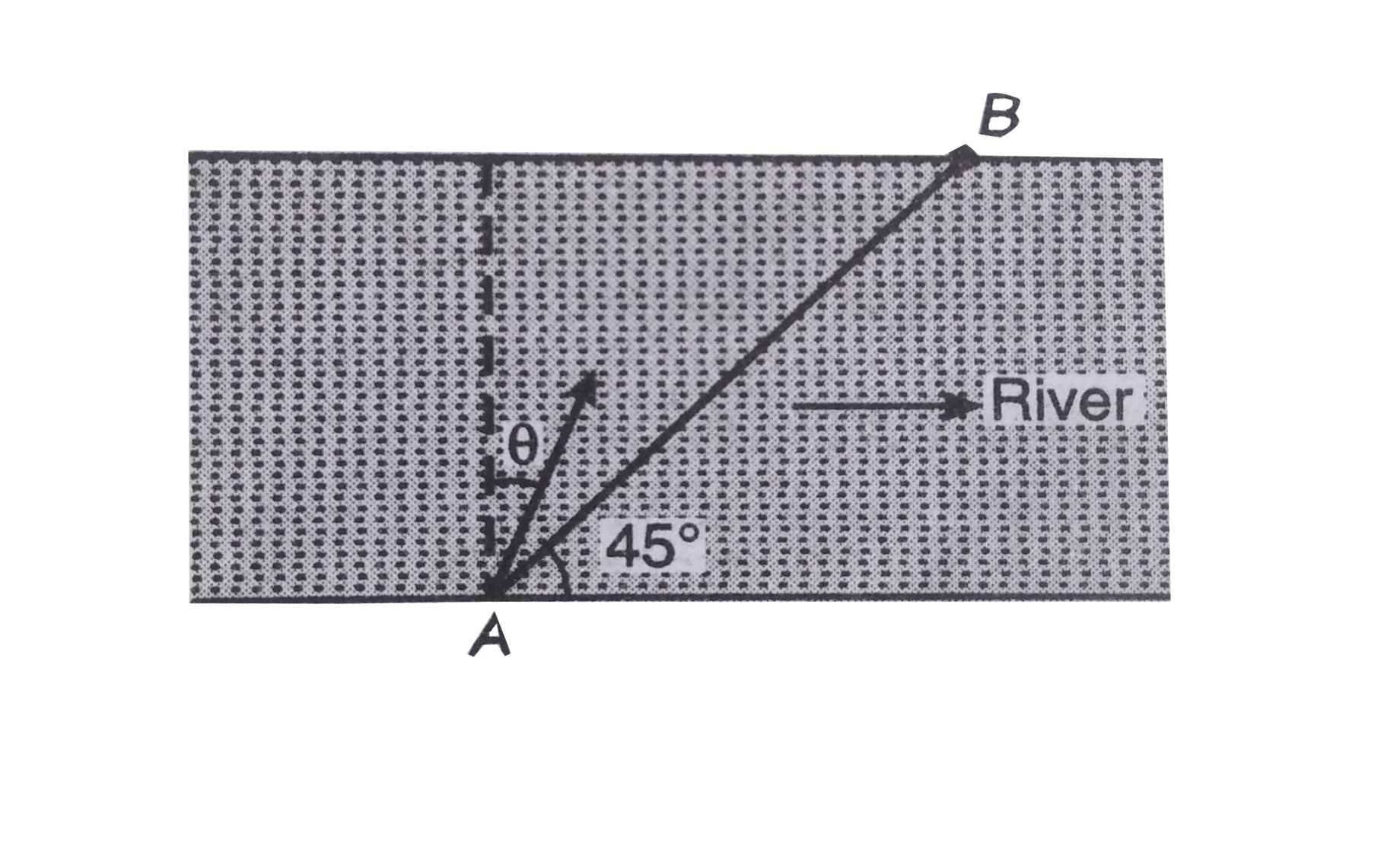
Given |Vbr|=4m/s= magnitude of velocity of boatman with respect to river, vr=2m/s in the directior shown. Boatman wants to reach from point A to point B. At what angle θ should he row his boat ?
The correct Answer is:A, B, C, D
Net velocity is along AB or at 45∘ if,
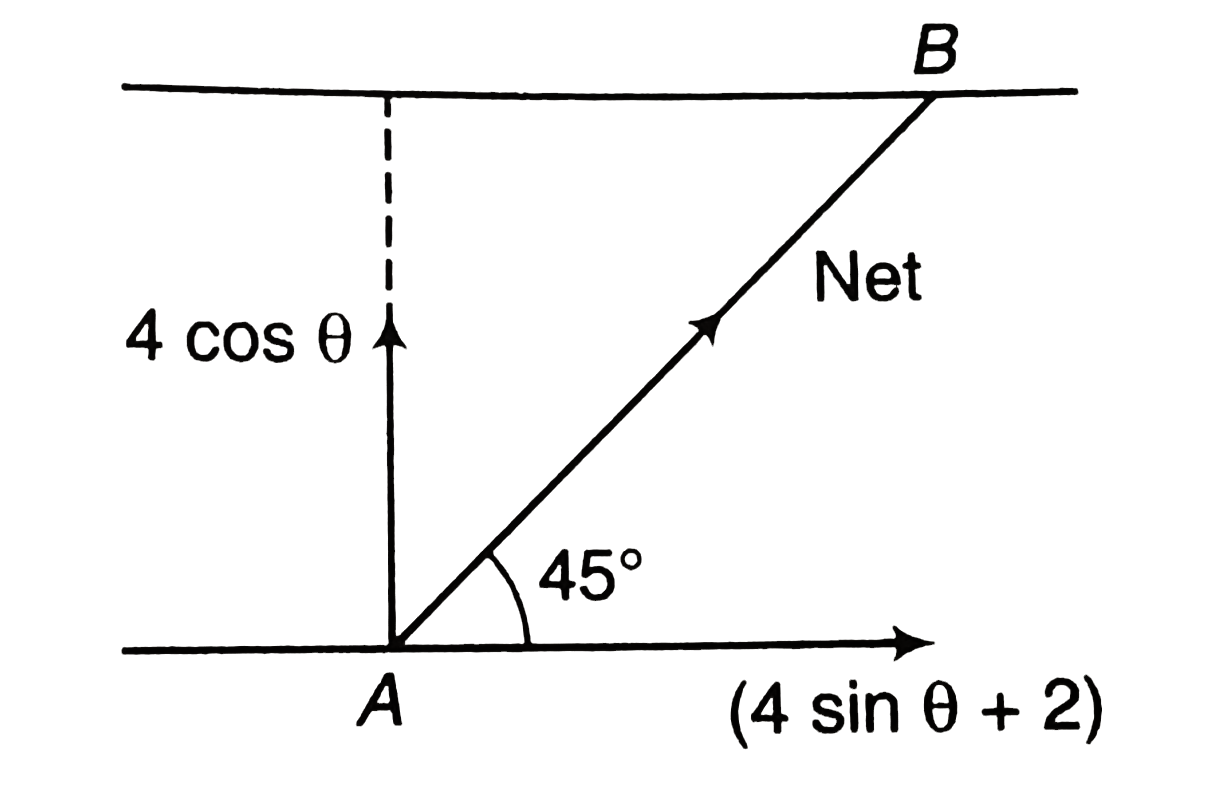
4cosθ=4sinθ+2
Solving this equation we get,
θ≈24.3∘
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Objective
Explore 45 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
Velocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C

View Solution
Knowledge Check
A boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
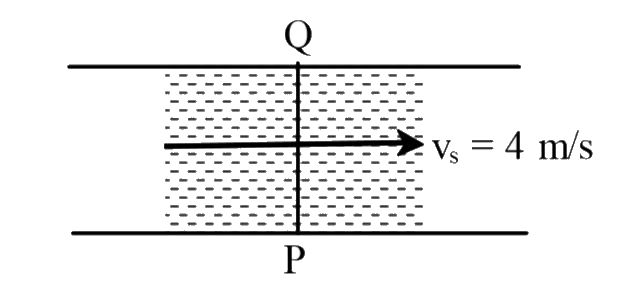 Aat right angle to the streamBat an angle of sin−1(2/5) with PQ up the streamCat an angle of sin−1(2/5) with PQ down the streamDat an angle cos−1(2/5) with PQ down the stream
Aat right angle to the streamBat an angle of sin−1(2/5) with PQ up the streamCat an angle of sin−1(2/5) with PQ down the streamDat an angle cos−1(2/5) with PQ down the streamA boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
 AAt right angle to the streamBAt an angle of sin−1(25) with PQ up the streamCAt an angle of sin−1(25) with PQ down the streamDAt an angle of cos−1(25) with PQ down the stream
AAt right angle to the streamBAt an angle of sin−1(25) with PQ up the streamCAt an angle of sin−1(25) with PQ down the streamDAt an angle of cos−1(25) with PQ down the streamA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
A30sB40sC50sD60s
A river 60m wide is flowing at a rate of 4m/s .A boat is sailing at a velocity of 20 m/s with respect to the river in a direction making an angle 37∘ with the direction of river flow.Find time taken by the boat in seconds to reach the opposite bank. (A) 2 (B) 3 (C) √6 (D) 5
View SolutionWidth of a river is 30m, velocity is 4m/s and rowing velocity is 5m/s
(a) Make the velocity diagram for crossing the river in shortest time. Then, find this shortest time, net velocity of boatman and drigt along the river.
(b) Can the boatman reach a point just oppsite on the other shore? If yes then make the velocity diagram, the direction in which the should row his boat and the time taken to cross the river in this case.
(c) How long will it iake hom to row 10m up the stream and then back to his starting point?
View SolutionA rever 500m wide flows at a rate at a rate of 4kmh−1. A swinmmer who can swin at 8kmh−1. In still water, wishes to cross the river straight . (i) Along what direection must he strike? (ii) What should be his resultant velocity. (ii) What is the time of crossing the river?
View SolutionVelocity of a swimmer with respect to a river is (ˆi+4ˆj)ms and velocity of the river flow is (2ˆj)ms then velocity of swimmer with respect to ground is (in m/s)
View SolutionVelocity of a boat relative to river current and river current velocity are equal in magnitude. Starting from point A on the southern bank, the boatman wants to reach a point B on the nothern bank in north−east from A. In which direction he has to steer the boat?

View Solution
