Two particles are moving along two long straight lines, in the same plane with same speed equal to 20cm/s. The angle between the two linse is 60∘ and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will be
50cm
40√2cm
50√2cm
50√3cm
The correct Answer is:D
To find the shortest distance between the two particles moving towards each other, we can follow the steps below:
1. Understand the Initial Setup:
- Let the two particles be A and B.
- Particle A is initially at a distance of 3 m from point O, and particle B is at a distance of 4 m from point O.
- The angle between the paths of the two particles is 60∘.
2. Define the Position Vectors:
- We can place point O at the origin (0, 0).
- The position of particle A can be represented as:
→RA=3^i(moving towards O)
- The position of particle B can be represented as:
→RB=4(cos60∘^i+sin60∘^j)=4(12^i+√32^j)=2^i+2√3^j
3. Calculate the Relative Position Vector:
- The relative position vector from A to B is given by:
→R=→RA−→RB=(3^i)−(2^i+2√3^j)=(3−2)^i−2√3^j=1^i−2√3^j
4. Determine the Velocities:
- Both particles are moving towards point O with a speed of 20 cm/s (0.2 m/s).
- The velocity of particle A is:
→VA=−20^i(moving towards O)
- The velocity of particle B can be resolved into components:
→VB=−20(cos60∘^i+sin60∘^j)=−20(12^i+√32^j)=−10^i−10√3^j
5. Calculate the Relative Velocity:
- The relative velocity of B with respect to A is:
→VBA=→VB−→VA=(−10^i−10√3^j)−(−20^i)=(10^i−10√3^j)
6. Find the Shortest Distance:
- The shortest distance occurs when the relative position vector is perpendicular to the relative velocity vector.
- The magnitude of the relative position vector is:
|→R|=√(1)2+(−2√3)2=√1+12=√13
- The magnitude of the relative velocity is:
|→VBA|=√(10)2+(−10√3)2=√100+300=√400=20
7. Calculate the Perpendicular Component:
- The perpendicular component of the relative position vector can be calculated using the formula:
R_{\perpendicular} = \sqrt{R^2 - R_{\parallel}^2}
- To find R∥, we can use the dot product:
R∥=→R⋅→VBA|→VBA|=(1)(10)+(−2√3)(−10√3)20=10+6020=7020=3.5
- Now, substituting back:
R_{\perpendicular} = \sqrt{13 - (3.5)^2} = \sqrt{13 - 12.25} = \sqrt{0.75} \approx 0.866 \text{ m}
8. Convert to Centimeters:
- The shortest distance between the two particles is:
0.866 m×100=86.6 cm
Final Answer
The shortest distance between the two particles will be approximately 86.6 cm.
- Let the two particles be A and B.
- Particle A is initially at a distance of 3 m from point O, and particle B is at a distance of 4 m from point O.
- The angle between the paths of the two particles is 60∘.
- We can place point O at the origin (0, 0).
- The position of particle A can be represented as:
→RA=3^i(moving towards O)
- The position of particle B can be represented as:
→RB=4(cos60∘^i+sin60∘^j)=4(12^i+√32^j)=2^i+2√3^j
- The relative position vector from A to B is given by:
→R=→RA−→RB=(3^i)−(2^i+2√3^j)=(3−2)^i−2√3^j=1^i−2√3^j
- Both particles are moving towards point O with a speed of 20 cm/s (0.2 m/s).
- The velocity of particle A is:
→VA=−20^i(moving towards O)
- The velocity of particle B can be resolved into components:
→VB=−20(cos60∘^i+sin60∘^j)=−20(12^i+√32^j)=−10^i−10√3^j
- The relative velocity of B with respect to A is:
→VBA=→VB−→VA=(−10^i−10√3^j)−(−20^i)=(10^i−10√3^j)
- The shortest distance occurs when the relative position vector is perpendicular to the relative velocity vector.
- The magnitude of the relative position vector is:
|→R|=√(1)2+(−2√3)2=√1+12=√13
- The magnitude of the relative velocity is:
|→VBA|=√(10)2+(−10√3)2=√100+300=√400=20
- The perpendicular component of the relative position vector can be calculated using the formula:
R_{\perpendicular} = \sqrt{R^2 - R_{\parallel}^2}
- To find R∥, we can use the dot product:
R∥=→R⋅→VBA|→VBA|=(1)(10)+(−2√3)(−10√3)20=10+6020=7020=3.5
- Now, substituting back:
R_{\perpendicular} = \sqrt{13 - (3.5)^2} = \sqrt{13 - 12.25} = \sqrt{0.75} \approx 0.866 \text{ m}
- The shortest distance between the two particles is:
0.866 m×100=86.6 cm
The shortest distance between the two particles will be approximately 86.6 cm.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Knowledge Check
Two particles are moving along a straight line as shown. The velocity of approach between A and B is
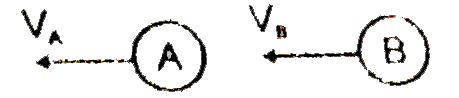 AVA+VBB|VA−VB|CVA−VBDVB−VA
AVA+VBB|VA−VB|CVA−VBDVB−VATwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 A50√3cmB300cmC100√3cmD200cm
A50√3cmB300cmC100√3cmD200cmFor two particles vibrating in the same phase, the minimum distance between them is called
AWavelengthBFrequencyCAmplitudeDPhase
Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles of equal mass are moving along the same line with the same speed in the same direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles A and B move with constant velocities v1 and v2 along two mutually perpendicular strainght lines. Towards the intersection point O. At moment t=0 the particle were located at distance l1 and l2 from O respectively. Find the time when they are nearest and also this shortest distance
View SolutionTwo unstable particles move in the reference frame K along a straight line in the same direction with a velocity v=0.990c. The distance between them in this reference frame is equal to l=120m. At a certain moment both particles decay simultaneously in the reference frame fixed to them. What time interval between the moments of decay of the two particles will be observed in the frame K? Which particle decays later in the frame K?
View SolutionTwo ships, 1 and 2, move with constant velocities 3 m/s and 4 m/s along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0 the ships were located at the distances 120 m and 200 m from the point O. How soon will the distance between the ships become the shortest and what is it equal to ?
View Solution