The position of a particle moving on X-axis is given by
x=At3+Bt2+Ct+D.
The numerical values of A,B,C,D are 1,4,-2 and 5 respectively and I units are used. Find a. the dimensions of A,B, C and D b. the velocity of the particle at t=4s, the acceleration of he particle at t=4s, d. The average velocity during the interval t=0 to t=4s, the average accelerationduring the interval t=0 to t=4s.Solution in Tamil
a. Dimensons of x, At3,Bt2,CtandD must be indentica and in this case each is length. Thus,
[At2]=L,or[A]=LT−3
[Bt&2]=L,or[B]=LT−2
[Ct]=L,or[C]=LT−1
and [D]=L
b. x=At3+Bt2+Ct+D
or, v=dxdt=3At2+2Bt+C
Thus at t=4s, the velocity <br>=3(1s3)(16s2)+(4ms2)(4s)+(−2ms)
=(48+32−2)ms=78ms
c. v=3At^2+2Bt+C<br>or,a=(dv)/(dt)=6At+2B.<br>At=2,a=6(1ms3)(4s)+2(4ms2)=32ms2
d. x=At3+Bt2+Ct+D
Position at t=0 is x=D =m<br>Positionatt=4sis<br>(m/s^3)(64s^3)+(4m/s^2)(16s^2)-(2m/s)(4s)+5m<br>=()64+64−8+5)m=125m
Thus, the displacement during 0 to 4 s is
125m−5m=120m
Average velocity =120m4s=30ms
e. v=3At2+2Bt+C
Velocity at t=0 is C=-2 m/s,
Velocity at t=4s is =78 m/s
Average acceleration =v2−v1t2−t1=20ms2.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer14videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -113videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises34videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
Similar Questions
Galileo was punished by the Church for teaching that the sum is stationary and the earth moves around it. His opponents held the view that the earth is stationary and the sun moves around it. If the absolute motion has no meaing,are the two view points not equally correct or equally wrong?
04:31View SolutionA motor car is going due north at a speed of 50 km/h. It makes a 900 left turn without changing the speed. The change in the velocity of the car is about
02:34View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
04:37View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
05:20View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
12:03View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
08:21View SolutionA particle is at x=5m at t=0,x=−7m at t=6s and x=+2m at t=10s, find the average velocity of the particle during the interval (a) t=0 to t=6s, (b) t=6s to t=10s, (c) t=0 to t=10s
11:43View SolutionThe position of a particle moving on X-axis is given by x=At2+Bt+C The numerical values of A, B and C are 7, -2 and 5 respectively and SI units are used. Find
(a) The velocity of the particle at t= 5
(b) The acceleration of the particle at t =5
(c ) The average velocity during the interval t = 0 to t = 5
(d) The average acceleration during the interval t = 0 to t = 505:02View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
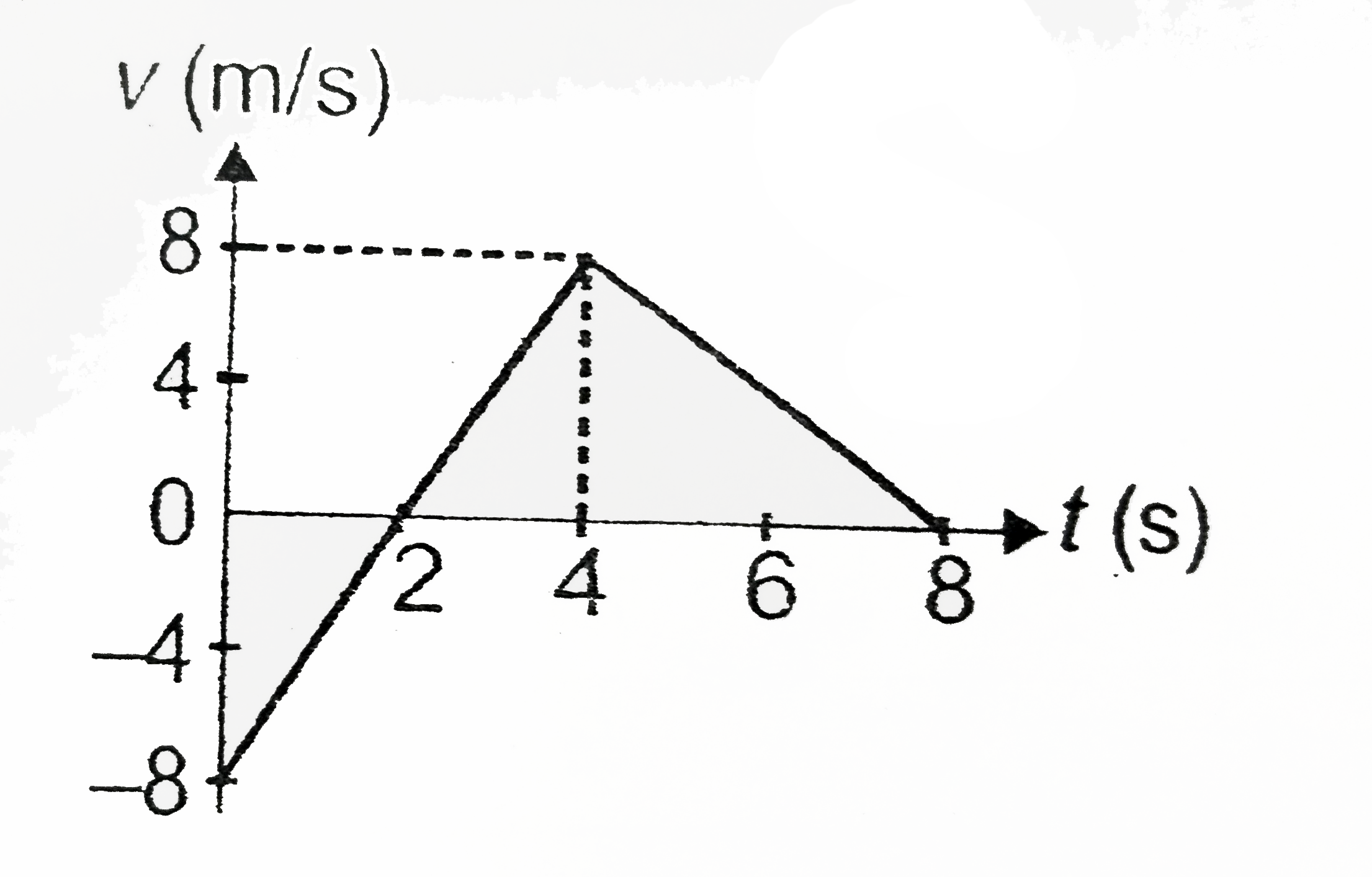
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.03:56View SolutionX-अक्ष के अनुदिश गति कर रहे कण की स्थिति निम्न समीकरण द्वारा व्यक्त है
x=At3+Bt2+Ct+D
जहां x मीटर में तथा t सेकण्ड में है। नियतांक A,B,C व D के आंकिक मान क्रमशः 1,4,-2 व 5 हैं ज्ञात कीजिए
(i) A,B,C व D के विमीय सूत्र।
(ii) t=4 सेकण्ड पर कण का वेग तथा त्वरण। 1
(iii) प्रथम 4 सेकण्ड में कण् का औसत वेग।
(iv) प्रथम 4 सेकण्ड में कण का औसत त्वरण।01:48View Solutionx -अक्ष पर चलते हुए एक कण का स्थान x=At3+Bt2+Ct+D के अनुसार बदलता है | SI इकाइयों में A, B, C एवं D के सांख्यिक मान क्रमशः 1,4,−2 तथा 5 है | (a) A, B, C तथा D के विमीय - सूत्र निकले | (b) समय t=4s पर कण का वेग निकालें | (c) t=4s पर कण का त्वरण निकालें | (d ) t=0 से t=4s के अंतराल में कण का औसत वेग निकाले | (e) t = 0 से t = 4s के अंतराल में कण का औसत त्वरण निकालें |
04:39View Solutionचित्र में x -अक्ष पर चलते हुए एक कण के वेग का समय के साथ ग्राफ दिखाया गया है |
(a) समय t =0 से t = 4s तक में कण की गति कैसी है, इसका वर्णन करे |
(b) पहले 2 सेकंड में कण द्वारा चली गई दुरी निकले |
(c ) t=2s से t=4s तक में चली गई दुरी निकले |
(d) t=0 से t=4s तक में चली गई दुरी निकाले |
(e) t=0 से t=4s तक में विस्थापन निकले |
(f) t=12s पर कण का त्वरण निकले |
(g) t=2s पर कण का त्वरण निकाले |
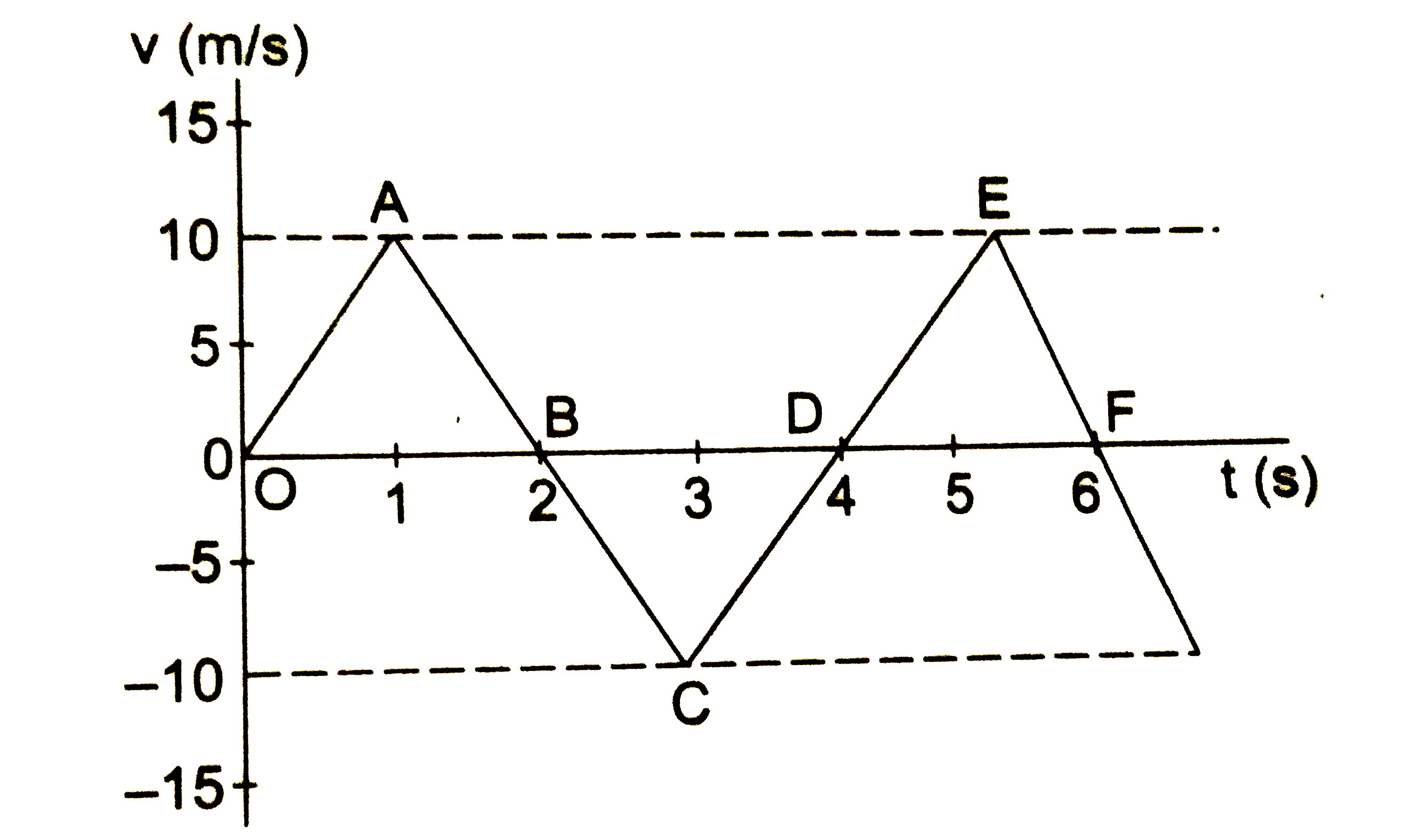 02:55View Solution
02:55View Solutionचित्र में x - अक्ष पर चलते हुए एक कण का x - निर्देशांक समय के फलां के रूप में दिखाया गया है | ज्ञात करे, (a) t = 0 से t = 10s के अंतराल में औसत वेग (b) 2, 5, 8 तथा 12 s पर कण के वेग |
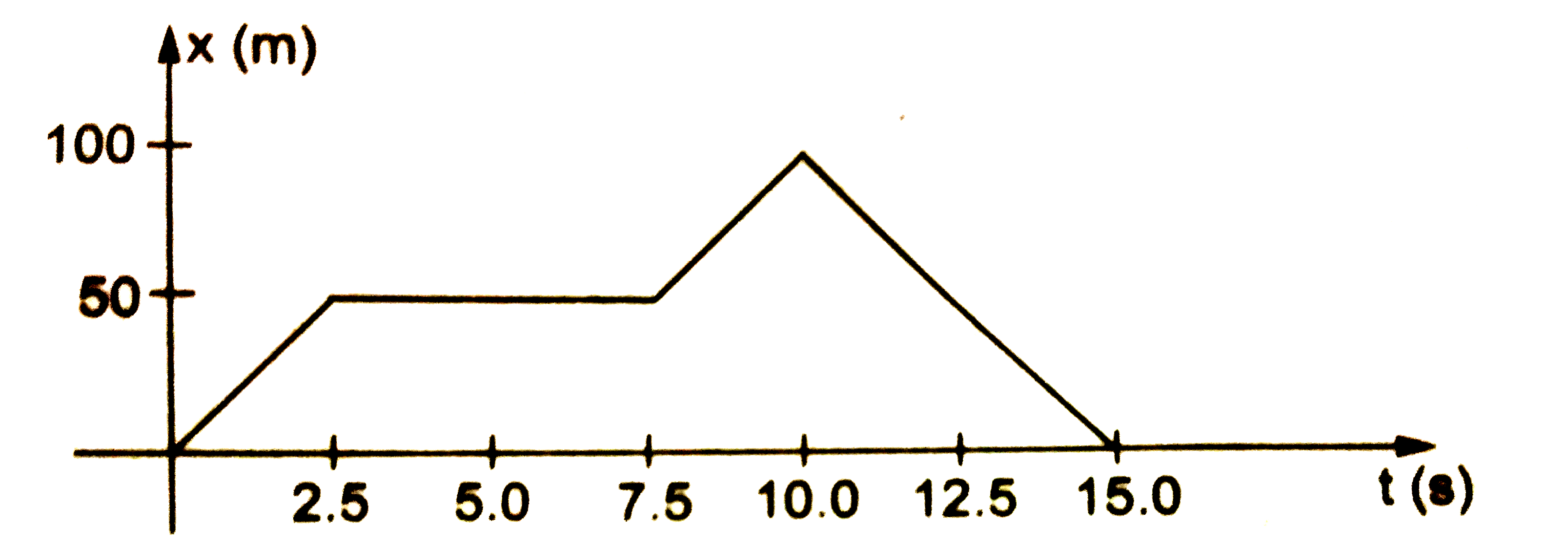 View Solution
View SolutionA particle is at x =+ 5 m at t =0,x =- 7 m at t = 6 s and x = + 2 at t = 10s. Find the average velocity of the particle during the intervals
(a)t=0 to t=6s
(b)t=6s to 6=10s
(c ) t=0 to t=10s .02:42View SolutionX-अक्ष पर गति करते हुए कण की स्थिति समीकरण x=At2+Bt+C से दी जाती है। A, B तथा C के संख्यात्मक मान क्रमशः 7,−2 और 5 SI इकाई में है, तो ज्ञात करो।
(a) t=5 पर कण का वेग
(b) t=5 पर कण का त्वरण04:10View SolutionA particle is at x=+5 m at t=0,
x=-7m at t=6 s and x =+2 at t=10s.Find the averahe velocity of the particle during the intervals
(a)t=0 to t=6s
(b)t=6s to t=10s,
©t=0 to t=10 s.02:20View Solution
