Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
BC
12BC
13BC
14BC
The correct Answer is:B
Step by step video & text solution for Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
View SolutionTwo circles are tangent internally at P and a chord, AB of the larger circle is tangent to the smaller circle at C. PB and PA cut the smaller circle at E and D, respectively. If AB = 15 cm, While PE = 2 cm and PD = 3 cm. Find AC
View Solution
Knowledge Check
Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
ABCB12BCC13BCD14BCTwo concentric circles with centre P have radii 6.5 cm and 3.3 cm. Through a point A of the larger circle, a tangent is drawn to the smaller circle touching it at B and the larger circle at C. find the length of the tangent
A5.6 cmB11.2 cmC11.8 cmD6.5 cm
In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
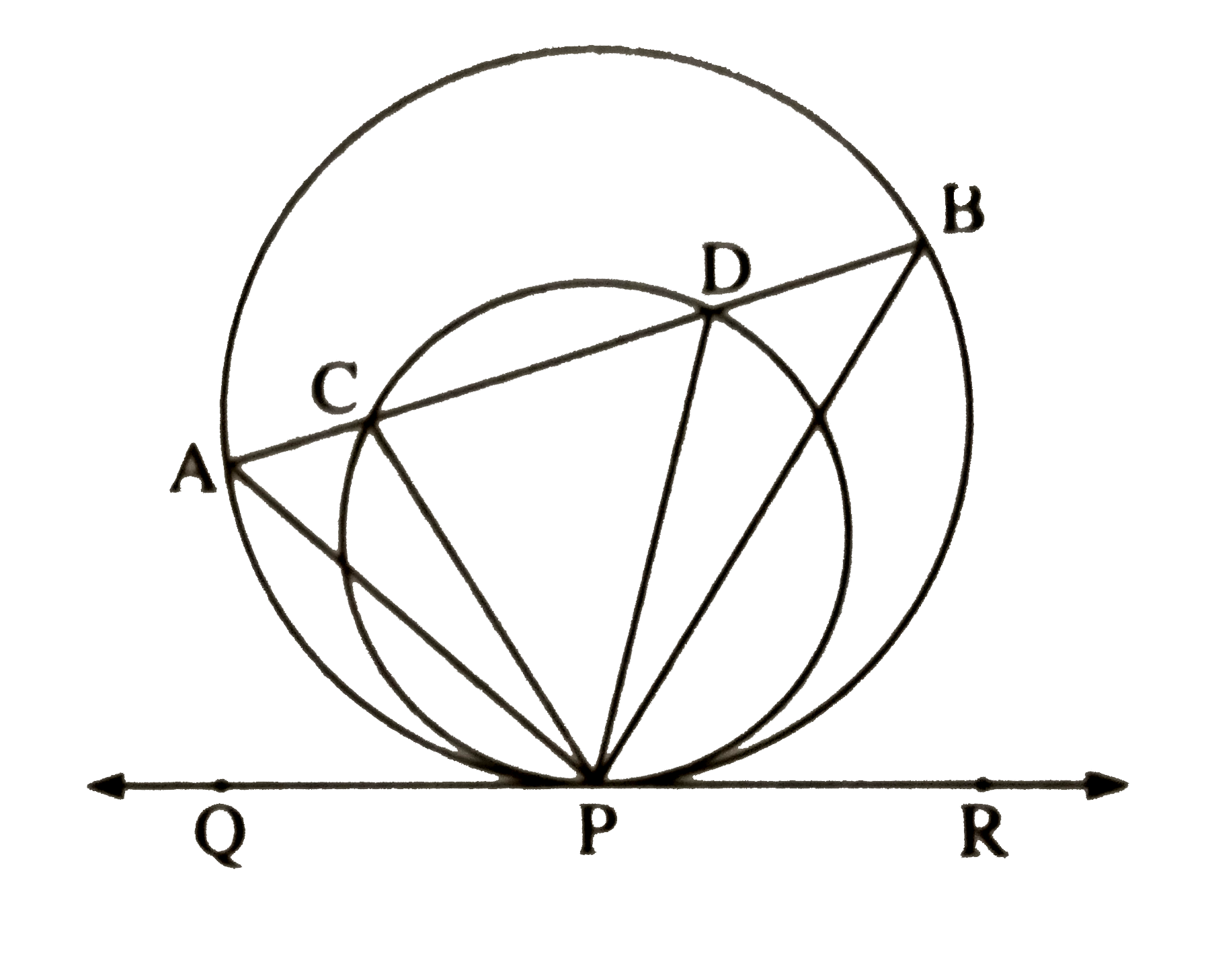
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View SolutionTwo chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of ∠BAC
View SolutionIn the figure, the radius of the larger circle is 2 cm and the radius of the smaller circle is 1 cm and the larger circle passes through the centre of the smaller circleThe length (in cm) of the chord AB is :
View SolutionIn two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View Solution
