Two circles with centres A and B touch each other internally. Another circle touches the larger circle internally at the point X and the smaller circle externally at the point Y. If O be the centre of that circle, prove that (OA + BO) is constant. Solution in Bengali
Let the circle with centre A touches the circle with centre B internally at the circle with centre B internally at the point C. We know that if two circles touches each other either externally or internally, then the centres of the circles and the point of contact lie on the same straight line.
∴ the points A, O, X, A, B, C and B, Y, O lie on the same straight line each.
Now, AO+BO+BY+OY [as per. figure]
=OA+OY+BY
=OA+OX+BY[∵OY=OX= radii of same circle]
=AX+BY [as per figure AO+OX=AX]
= Radius of hte larger circle + Radius of the smaller circle.
= Constant [∵ both the circles are fixed ]
Hence (AO+BO) = constant (Proved)

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO TANGENT IN A CIRCLE Exercise:EXERCISE 4.1
Explore 20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO TANGENT IN A CIRCLE Exercise:EXERCISE 4.2
Explore 23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBook:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO ANGLES IN A CIRCLEExercise:EXERCISE 2.3 (Long Answer Type Questions)
Explore 14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES Book:CALCUTTA BOOK HOUSEChapter:TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES Exercise:EXERCISE
Explore 66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionIf two circles touch each other (internally or externally); the point of contact lies on the line through the centres.
View SolutionIn the given figure two small circles touch each other externally at the centre of a big circle and these small circles are touched internally by a big circle of radius 74cm. Find the area of the shaded region

View SolutionProve that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
View SolutionThe locus of the centre of the circle that touch a given circle internally is ________
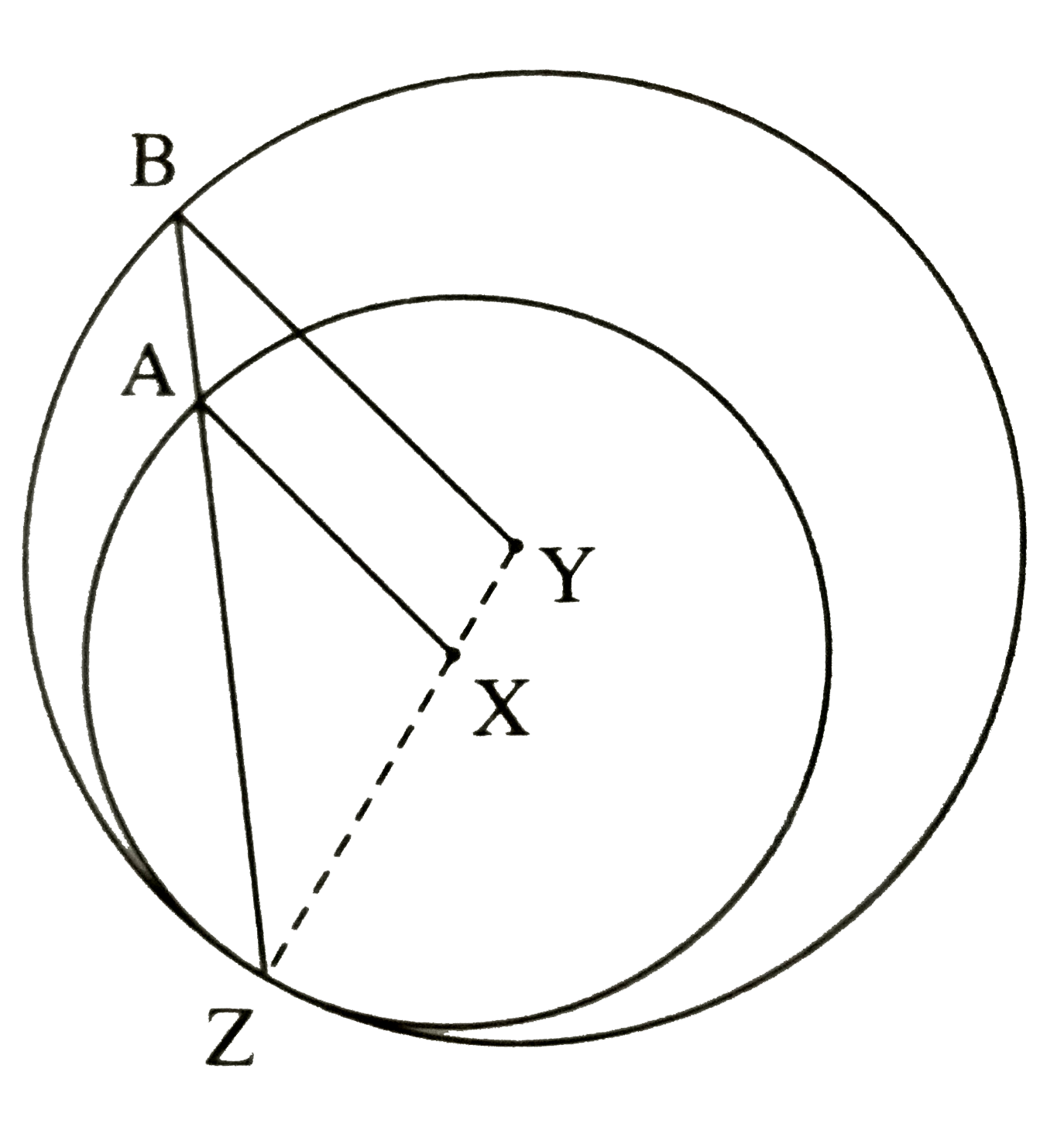
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
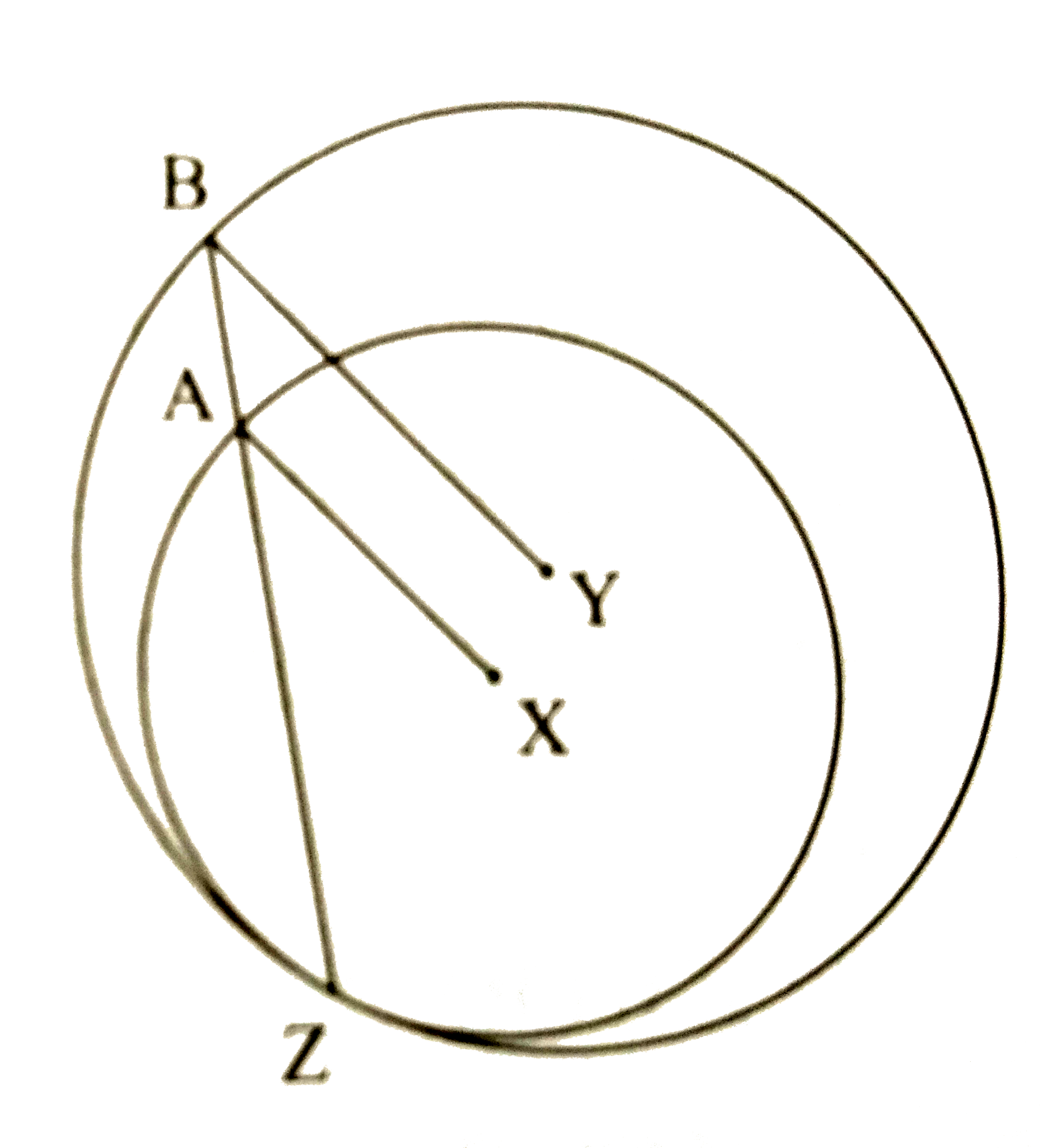
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
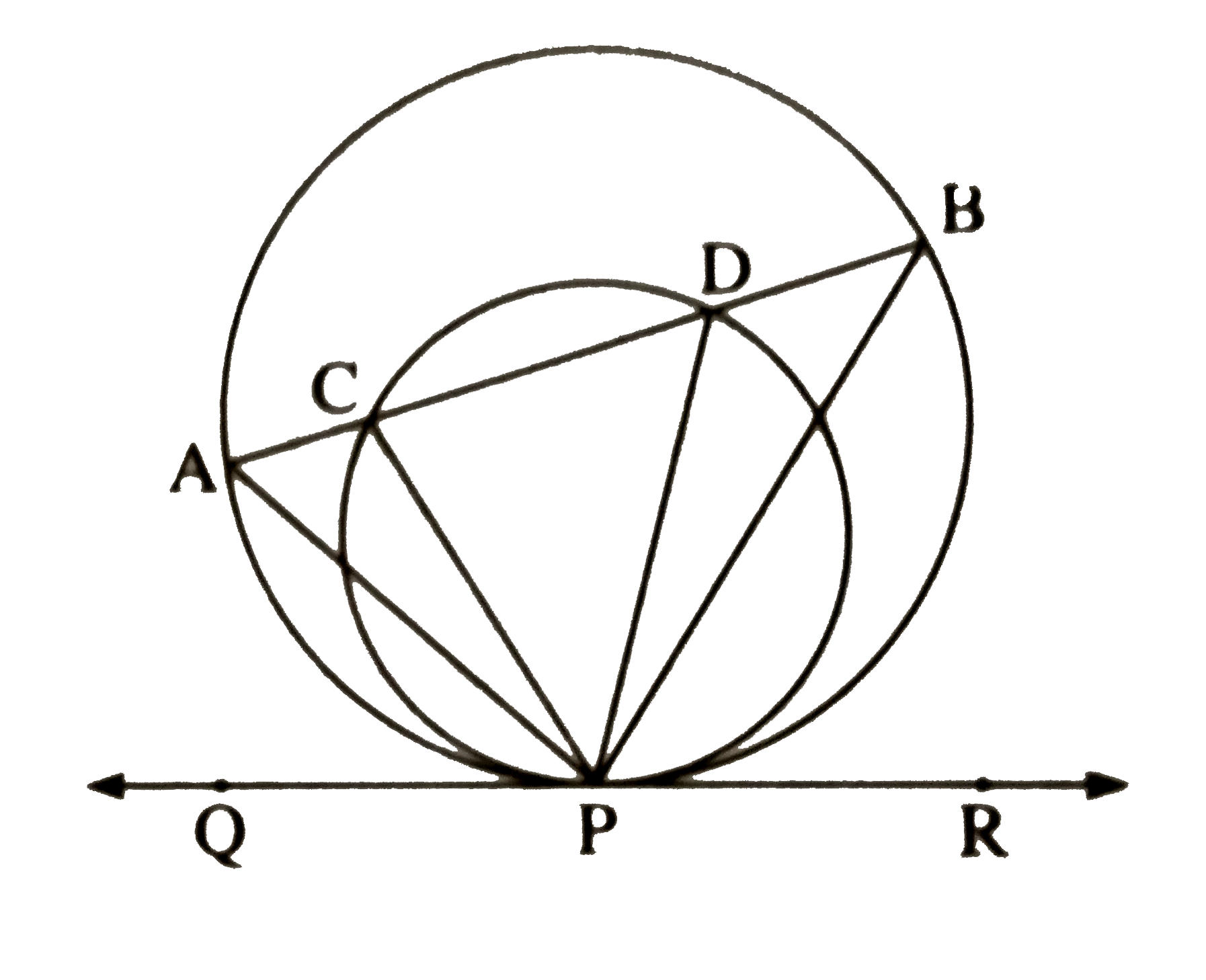
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
View SolutionTwo circle with centre O and P intersect each other in point C and D. Chord AB of the circle with centre O touches the circle with circle with centre P in Point E. Prove that ∠ADE+∠BCE=180∘
View Solutionदिये चित्र में दो छोटे वृत्त एक - दूसरे को बड़े वृत्त के केंद्र पर बाह्यतः स्पर्श करते है और ये छोटे वृत्त , बड़े वृत्त द्वारा अन्तः स्पर्श होते है । बड़े वृत्त की त्रिज्या 4 सेमी है । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।

View SolutionIn the given figure, there are two circles with the centres O and O' touching each other internally at P. Q Tangents TQ and TP are drawn to the larger circle and tangents TP and TR are drawn to the smaller circle. Find TQ:TR :

View SolutionA smaller circle touches internally to a larger circle at A and passes through the centre of the larger circle. O is the centre of the larger circle and BA, OA are of the diameters of the larger and smaller circles respectively. Chord AC intersects the smaller circle at a point D. If AC = 12 cm , then AD is :
View Solution

