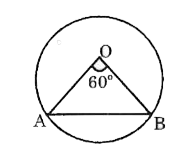
The angle subtended by a chord at its centre is 60∘, then the ra tio between chord and radius is
1:2
1:1
√2:1
2:1
The correct Answer is:B
OA = OB
⇒∠OAB=∠OBA
⇒∠OAB=180∘−60∘2
⇒∠OAB=60∘
अत: ΔOAB एक समबाहु Δ है।
∴OA=OB=AB
thereoeOA:AB=1:1
Similar Questions
State and prove that:
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
View SolutionThe chord of a circle is √3 times its radius. The angle subtended by this chord at the minor arc is k times the angle subtended at the major arc. What is the value of k ?
View Solution
Knowledge Check
The angle subtended by a chord at its centre is 60∘, then the ratio between chord and radius is
A1:2B1:1C√2:1D2:1Calculate the angle subtended by the chord at the point on the major arc if the radius and the chord of the circle are equal in length
AA) 30∘BB) 120∘CC) 200∘DD) 300∘A chord of length 10 cm subtends an angle 120∘ at the centre of a circle . Distance of the chord from the centre is
A5√3B6√3C4√3D52√3
If the angle subtended by two chords of a circle at the centre are equal; the chords are equal.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionAngle Subtended By A Chord At A Point|NCERT Exercise
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc
View Solution
