The angle subtended at the centre of a circle , by a chord whose length is equal to the radius of the circle will be Solution in Bengali
πc3
πc4
662g3
50g
The correct Answer is:A,C
Step by step video, text & image solution for The angle subtended at the centre of a circle , by a chord whose length is equal to the radius of the circle will be by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MEASURMENT OF TRIGONOMETRICAL ANGLESBOOK - CHHAYA PUBLICATIONCHAPTER - MEASURMENT OF TRIGONOMETRICAL ANGLESEXERCISE - Sample Questions for Competitive Exams (Integer Answer Type )
5 Videos
- MEASURMENT OF TRIGONOMETRICAL ANGLESBOOK - CHHAYA PUBLICATIONCHAPTER - MEASURMENT OF TRIGONOMETRICAL ANGLESEXERCISE - Sample Questions for Competitive Exams (Comprehension Type)
6 Videos
- MEASURMENT OF TRIGONOMETRICAL ANGLESBOOK - CHHAYA PUBLICATIONCHAPTER - MEASURMENT OF TRIGONOMETRICAL ANGLESEXERCISE - EXERCISE 1
50 Videos
- MEASURES OF DISPERSION BOOK - CHHAYA PUBLICATIONCHAPTER - MEASURES OF DISPERSION EXERCISE - Sample question for competitive exams (D. Assertion-Reason Type)
2 Videos
- METHOD OF SUBSTITUTIONBOOK - CHHAYA PUBLICATIONCHAPTER - METHOD OF SUBSTITUTIONEXERCISE - Sample Questions for Competitive Examination (Assertion-Reason Type)
2 Videos
Similar Questions
The angles of a triangle are in A.P . If the greatest and the least of them be nπ4and100g3 respectively , then the value of n will be
View SolutionLet D be the number of degrees , R be the number of radian and G be the number of grades of any angle of the trianlge ABC.
Then the required relation among three systems of measurement of an angle is D90=G100=2Rπ .
If ∠A=30∘ then which one is true?
View SolutionA radian is a
View SolutionStatement - I :Mean of square of first n natural numbers is (n+1)(2n+1)6
Statement - II : Σn=n(n+1)2
View SolutionStatement-I: ∫x+1x(1+xex)2dx=11+xex+log∣∣∣xex1+xex∣∣∣+c where c is a real number.
Statement-II: ddx(xex)=(x+1)ex.
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionState and prove that:
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
View SolutionProve that if chords of congruent circles subtend equal angles at their centre then the chords are equal.
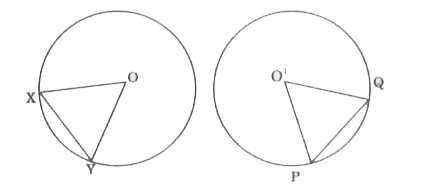
View SolutionProve that if chords of congruent circles subtend equal angles at their centres then chords are equal.
View SolutionIf the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
View Solution
