A rod of height H having mass μ is hangingvertically from ceiling. Find expansion at end of rod. Given young's modulus Y, cross section A. 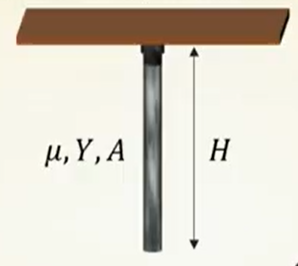
μgHAY
μgH2AY
μgH4AY
2μgHAY
Step by step video & image solution for A rod of height H having mass mu is hangingvertically from ceiling. Find expansion at end of rod. Given young's modulus Y, cross section A. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionTwo point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
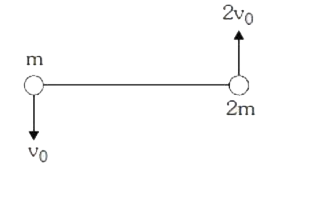
View Solution
Knowledge Check
A rod has length L0 at a reference temperature T0, coefficient of linear expansion α, Young's modulus Y, area of cross section A. Rod lie unconstrained on a smooth surface temperature of rod is increased bby ΔT. Mark the correct statement
AFinal length of rod is given by L=L0(1+αΔT) for all the range of values of α.BIf average coefficient of linear expansion is constant as L varies the general expression for the final length is L=L0eαΔTCRod is unstrained as it expandsDCoefficient of expansion is defined as α=1LdLdtA steel rod of length L0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through ΔT is (coefficient of linear expansion of steel is α and young's modulus for steel is Y ).
AYAαΔTB1/2YAαΔTC2YAαΔTD3YAαΔTA metallic rod of length l and cross - sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
AyB1yCy2D1y2
Two same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
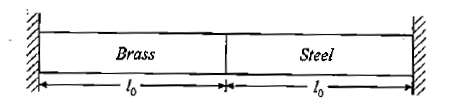
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composte rod increases by 1.91mm. When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

View SolutionA uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
View SolutionA metal bar of length L and area of cross-section A is clamped between two rigid supports. For the material of the rod. It Young's modulus is T and Coefficient if linear expansion is α. If the temperature of the rod is increased by Δt∘C, the force exerted by the rod on the supports is
View Solution

