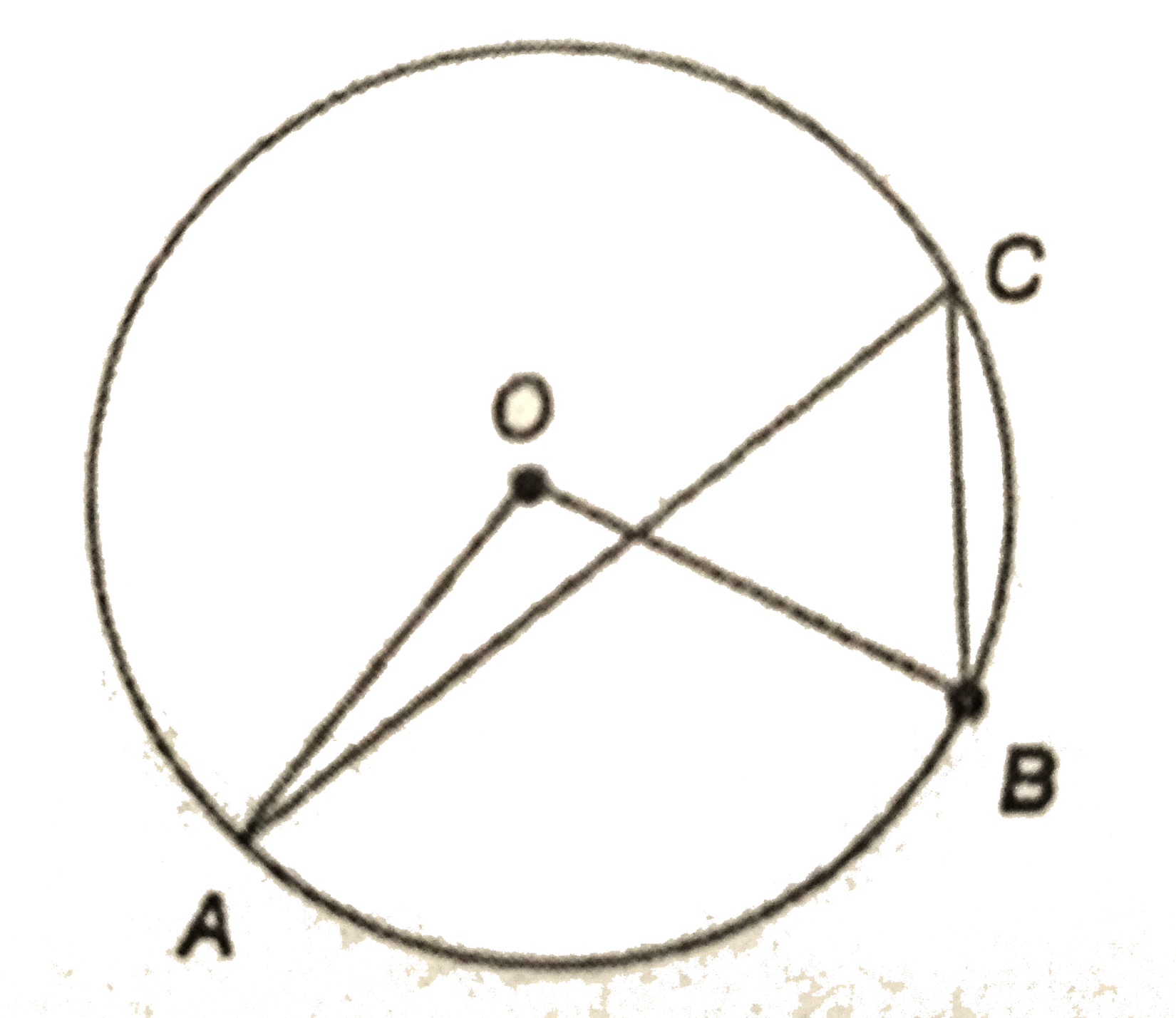A circle with centre O is given and C is a point on its minor arc AB. If ∠AOB=100∘ then ∠ACB is equal to which of the following?
A)80∘
B)90∘
C)100∘
D)130∘
The correct Answer is:D
To solve the problem, we need to find the value of angle ACB given that angle AOB is 100 degrees.
1. Understanding the Circle and Angles:
We have a circle with center O, and points A and B lie on the circumference of the circle. The angle AOB is given as 100 degrees.
2. Identifying the Minor and Major Arcs:
Since C lies on the minor arc AB, we can also identify the major arc AB. The total angle around point O is 360 degrees. Therefore, the angle corresponding to the major arc AB can be calculated as:
Angle of Major Arc AOB=360∘−Angle AOB=360∘−100∘=260∘
3. Finding the Angle ACB:
The angle ACB is an inscribed angle that subtends the same arc AB. The inscribed angle theorem states that an inscribed angle is half of the central angle that subtends the same arc. Therefore:
Angle ACB=12×Angle AOB=12×100∘=50∘
4. Conclusion:
Thus, the measure of angle ACB is 50 degrees.
Final Answer:
Angle ACB = 50 degrees.
We have a circle with center O, and points A and B lie on the circumference of the circle. The angle AOB is given as 100 degrees.
Since C lies on the minor arc AB, we can also identify the major arc AB. The total angle around point O is 360 degrees. Therefore, the angle corresponding to the major arc AB can be calculated as:
Angle of Major Arc AOB=360∘−Angle AOB=360∘−100∘=260∘
The angle ACB is an inscribed angle that subtends the same arc AB. The inscribed angle theorem states that an inscribed angle is half of the central angle that subtends the same arc. Therefore:
Angle ACB=12×Angle AOB=12×100∘=50∘
Thus, the measure of angle ACB is 50 degrees.
Angle ACB = 50 degrees.
Topper's Solved these Questions
- CIRCLE AND ITS TANGENT LINESBook:LUCENT PUBLICATIONChapter:CIRCLE AND ITS TANGENT LINESExercise:EXERCISE 8B
Explore 27 Videos
- CIRCLE AND ITS TANGENT LINESBook:LUCENT PUBLICATIONChapter:CIRCLE AND ITS TANGENT LINESExercise:EXERCISE 8B
Explore 27 Videos
- CENTRE OF TRIANGLEBook:LUCENT PUBLICATIONChapter:CENTRE OF TRIANGLEExercise:EXERCISE-6B
Explore 8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES Book:LUCENT PUBLICATIONChapter:CONGRUENCE AND SIMILAR TRIANGLES Exercise:EXERCISE-5B
Explore 8 Videos
Similar Questions
Knowledge Check
C is a point on the minor arc AB a circle with centre O. If ∠AOB=100∘, what is ∠ACB ?
A80∘B90∘C100∘D130∘In a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
A30∘B25∘C50∘D60∘In a circle with centre P, AB is a minor arc. Point Ris a point other than A and B on major arc AB. If ∠ARB=80∘, then ∠APB=........
A40∘B80∘C160∘D60∘
In the given figure, AOB is a diameter of a circle and CD||AB. If ∠BAD=30∘, then ∠CAD = ?

View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View SolutionIn the figure , O is the centre and ∠ACB=20∘∠AOD is equal to

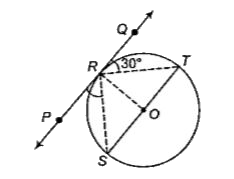
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
View SolutionO is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to

View Solution