The position of a projectile launched from the origin at t = 0 is given by s=(40ˆi+50ˆj)mat t=2s. if the projectile was launched at an angle θ from the horizontal, then θis (take g = 10 ms–2
tan−123
tan−132
tan−174
tan−145
The correct Answer is:C
Step by step video, text & image solution for The position of a projectile launched from the origin at t = 0 is given by s=(40hati+50hatj)mat t=2s. if the projectile was launched at an angle theta from the horizontal, then thetais (take g = 10 ms^(–2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The position of a projectile launched from the origin at t = 0 is given by vacr=(40ˆi+50ˆj)mat t=2s. if the projectile was launched at an angle θ from the horizontal, then θis (take g = 10 ms–2
View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range
View Solution
Knowledge Check
The position of a projectile launched from the origin at t = 0 is given by s=(40ˆi+50ˆj)mat t=2s. if the projectile was launched at an angle θ from the horizontal, then θis (take g = 10 ms–2
Atan−123Btan−132Ctan−174Dtan−145When a projectile is fired at an angle θ w.r.t horizontal with velocity u, then its vertical component:
Aremains sameBgoes on increasing with heightCgoes on decreasing with heightDfirst increase then decreases with heightA projectile is fired from the origin with a velocity v0 at an angle θ with x-axis. The speed of the projectile at an altitude h is .
Av0cosθB√v20−2ghC√v20sin2θ−2ghDNone of these
The range of a projectile when launched at angle θ is same as when launched at angle 2θ. What is the value of θ ?
View SolutionA projectile is projected with a speed of 40m/s at a angle θ with horizontal such that tanθ=34. After 2 sec, the projectile is moving with speed v at an angle α with horizontal then, (g=10m/s2)
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View SolutionThe highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of 15.0∘ above the horizontal. What is the projectile's launch speed?
View SolutionTwo projectiles are launched from a building of height 'h' as shown in the figure. One is launched at angle θ above horizontal and the other at angle θ below horizontal. Both the projectiles have same initial speed u. Which of the following is /are correct?
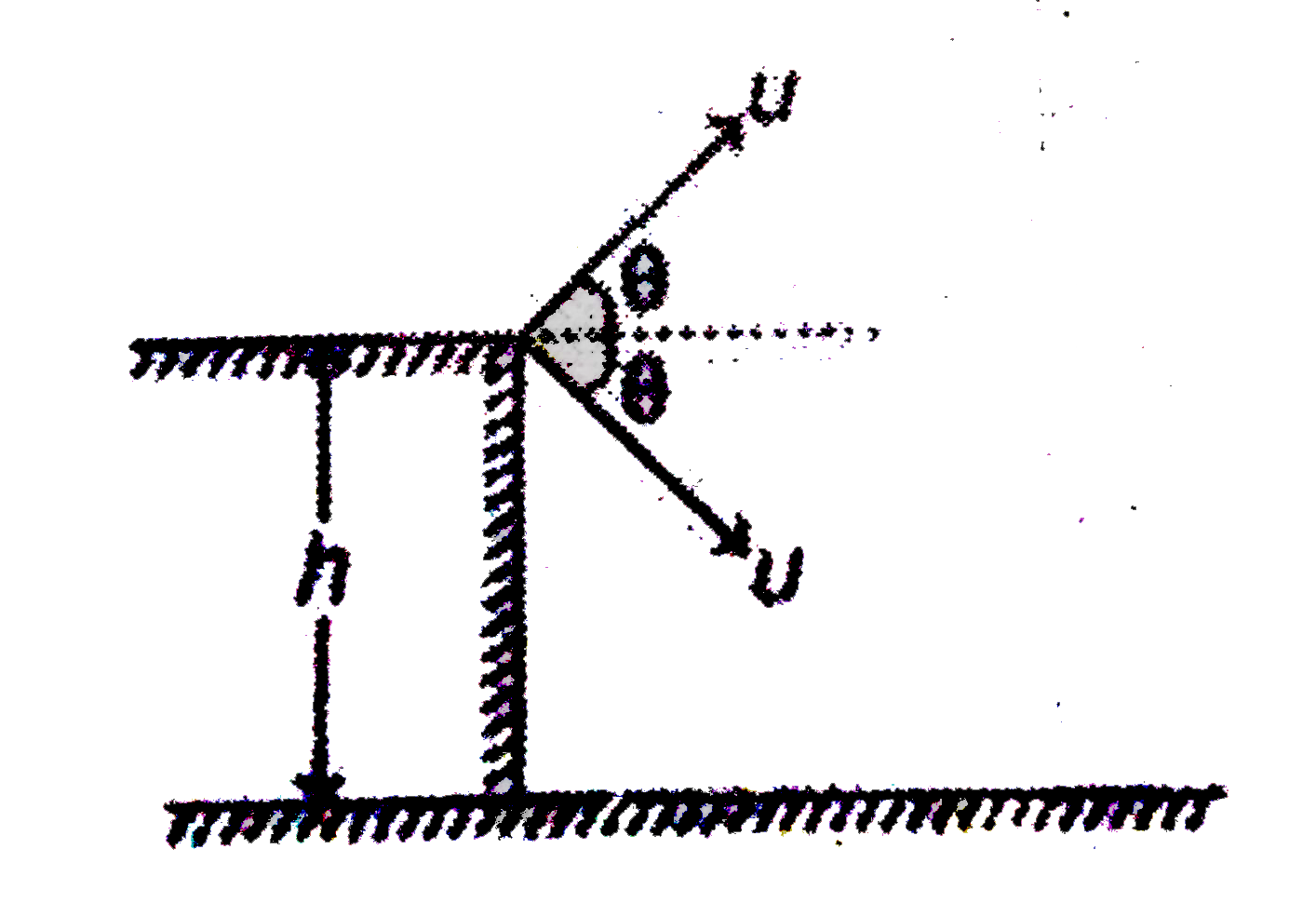
View Solution

