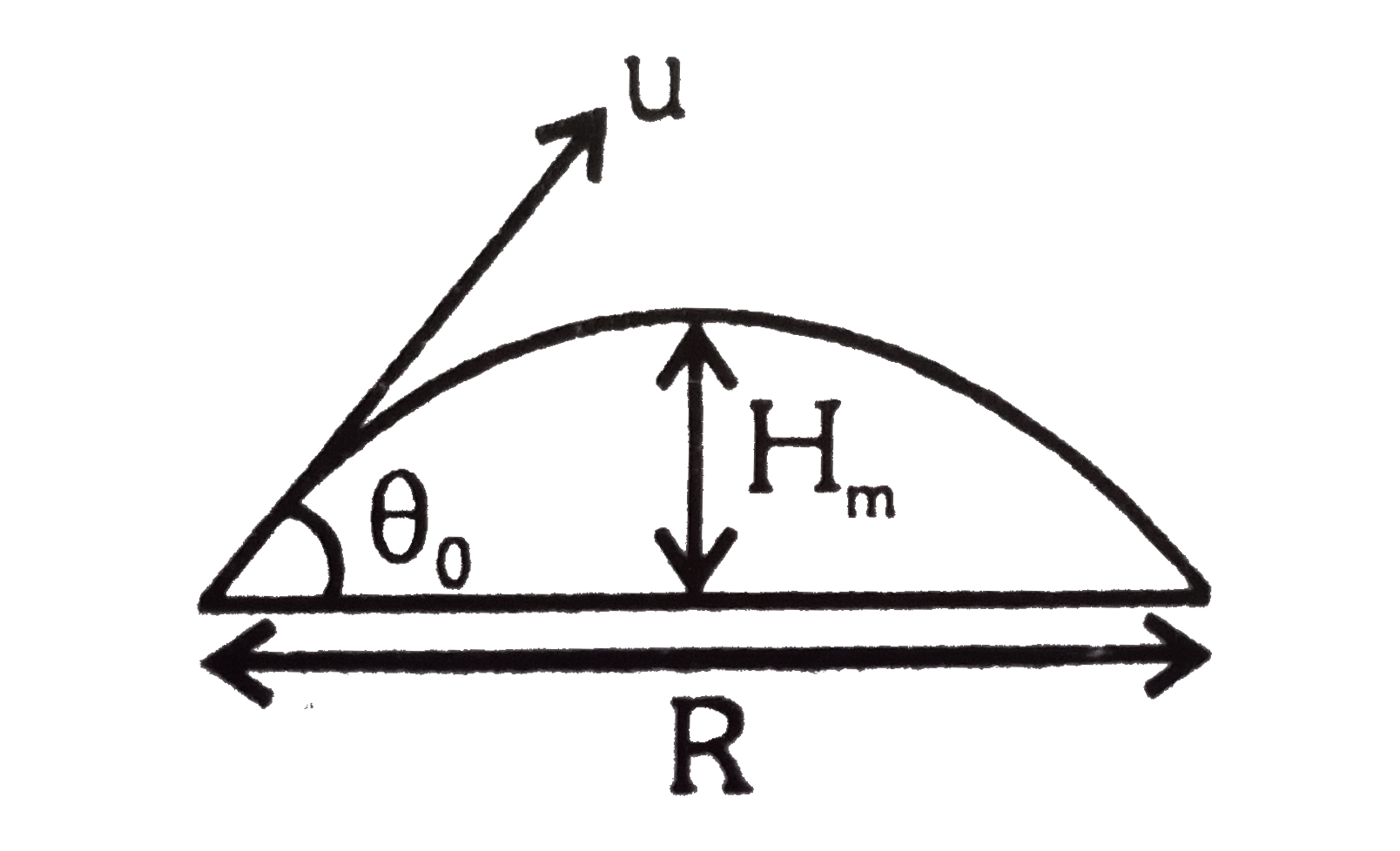
Show that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range
Hm=u2sin2θ02g and R=2u2g×sinθ0×cosθ0
So, HmR=tanθ04⇒tanθ0=4HmR⇒=tan−1(4HmR)
Topper's Solved these Questions
Similar Questions
(a) Show that for a projectile the angle between the velocity and the X-axis as a function of time is given by
θ(t)=tan−1[voy−gtvox]
(b) Show that the projection angle θ0 for a projectile lunched from the origin is given by θ0=tan−1(4hmR),
where the symbols have their usual meanings .View Solution(a) Show that for a projectile the angle between the velocity and the x-axis as function of time is given
by theta_(t) = tam ^(-1) ( 9 4 h_m)/R)
where the sybols have thir usual meanings.View Solution
Knowledge Check
- Question 1 - Select One
The position of a projectile launched from the origin at t = 0 is given by s=(40ˆi+50ˆj)mat t=2s. if the projectile was launched at an angle θ from the horizontal, then θis (take g = 10 ms–2
Atan−123Btan−132Ctan−174Dtan−145 - Question 2 - Select One
Two bodies are thrown from the same point with the same velocity of projection angles of projection being complimentary angles. If R1andR2 are the ranges and h1andh2 are maximum heights respectively, then
AR1=R2=u2gsin2θBh1+h2=u22gCbothDnone - Question 3 - Select One
A ball is projected with speed u at an angle θ to the horizontal. The range R of the projectile is given by
R=u2sin2θg
for which value of θ will the range be maximum for a given speed of projection? (Here g= constant)Aπ2radBπ4radCπ3radDπ6rad
Find the angle of projection for a projectile motion whose rang R is (n) time the maximum height H.
View SolutionThe position of a projectile launched from the origin at t = 0 is given by vacr=(40ˆi+50ˆj)mat t=2s. if the projectile was launched at an angle θ from the horizontal, then θis (take g = 10 ms–2
View SolutionA particle is projected with velocity u at angle θ1 with horizontal .The ratio of range and maximum height is 4. When it is projected at angle θ2 with horizontal with same speed,the ratio of range and maximum height is 2.Then tanθ1tanθ2 will be equal to
View SolutionIf h1 and h2 be the greatest heights in the two paths of a projectile and a given horizontal range R, then R=4h1h2.
View SolutionProve that for a projectile fired from level ground at an angle θ above the horizontal, the ratio of the maximum height H to the range R is given by
HR=14tanθView Solution

