A projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
A
452m
B
454m
C
432m
D
434m
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for A projectile is projected from the ground by making an angle of 60^@ with the horizontal. After 1 s projectile makes an angle of 30^@ with the horizontal . The maximum height attained by the projectile is (Take g=10 ms^-2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Practice Problems
- Question 1 - Select One
A projectile is projected at 10ms−1 by making an angle 60∘ to the horizontal. After sometime, its velocity makes an angle of 30∘ to the horzontal . Its speed at this instant is:
A10√3B10√3C5√3D5√3 - Question 1 - Select One or More
A projectile is projected from the ground making an angle of 30∘ with the horizontal.Air exerts a drag which is proportional to the velocity of the projectile
Aat highest point velocity will be horizontalBthe time of ascent will be equal to the time of descentCThe time of descent will be greater than the time of ascentDthe time of ascent will be greater than the time of descent - Question 1 - Select One
A projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
A√3secB1/√3secC(√3−1secDNone of these - Question 1 - Select One
A projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
Aucosθ2BucosθCu(2cos(θ)2−sec(θ)2)Du(cos(θ)2−sec(θ)2) - Question 1 - Select One
A ball is projected from the ground at a speed of 10ms−1 making an angle of 30∘ with the horizontal. Another ball is simultaneously released from a point on the vertical line along the maximum height of the projectile. The initial height of the second ball is
(Take g=10ms−2)A6.25 mB2.5 mC3.75 mD5 m - Question 1 - Select One
A particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
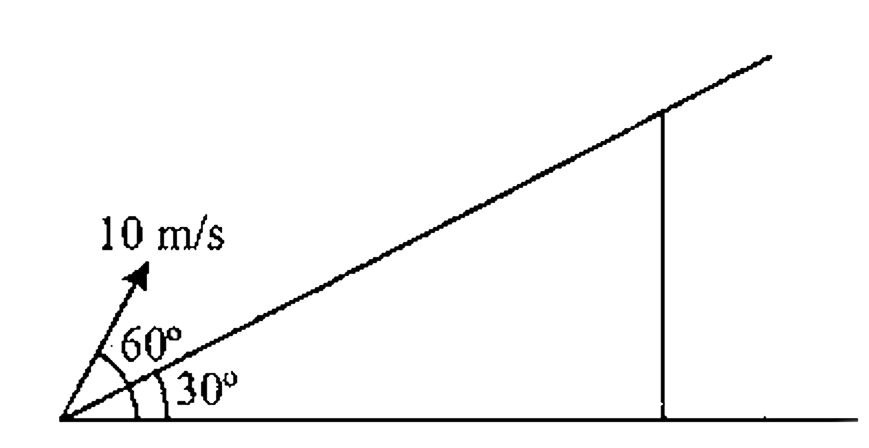 A2√3 secB1√3 secC√3 secD12√3 sec
A2√3 secB1√3 secC√3 secD12√3 sec - Question 1 - Select One
Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5 - Question 1 - Select One
A particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
 A2√3sB1√3sC√3sD12(√3)s
A2√3sB1√3sC√3sD12(√3)s - Question 1 - Select One
The angle of projection at which the horizontal range and maximum height of projectile are equal is
A45∘Bθ=tan−1(0.25)Cθ=tan−1(4)D60∘

