Two different sides of a parallelogram are 8 cm and 6 cm and the ratio of the diagonals is 3 : 4. Find the difference between the lengths of the diagonals?
5 cm
7 cm
8 cm
√8cm
The correct Answer is:D
To solve the problem step by step, we will follow these instructions:
Step 1: Define the diagonals
Let the lengths of the diagonals of the parallelogram be represented as:
- Diagonal 1 = 3x
- Diagonal 2 = 4x
Step 2: Use the formula for diagonals in a parallelogram
The relationship between the sides and diagonals of a parallelogram is given by the formula:
d21+d22=2(a2+b2)
where d1 and d2 are the lengths of the diagonals, and a and b are the lengths of the sides.
Step 3: Substitute the values
Given that the sides of the parallelogram are 8 cm and 6 cm, we can substitute these values into the formula:
(3x)2+(4x)2=2(82+62)
Step 4: Calculate the squares
Calculating the squares:
(3x)2=9x2
(4x)2=16x2
Thus, we have:
9x2+16x2=2(64+36)
Step 5: Simplify the equation
Combine the left side:
25x2=2(100)
This simplifies to:
25x2=200
Step 6: Solve for x
Now, divide both sides by 25:
x2=20025=8
Taking the square root gives:
x=√8=2√2
Step 7: Find the lengths of the diagonals
Now, we can find the lengths of the diagonals:
- Diagonal 1 = 3x=3(2√2)=6√2
- Diagonal 2 = 4x=4(2√2)=8√2
Step 8: Calculate the difference between the diagonals
The difference between the lengths of the diagonals is:
Difference=8√2−6√2=2√2
Final Answer
The difference between the lengths of the diagonals is 2√2 cm.
---
Let the lengths of the diagonals of the parallelogram be represented as:
- Diagonal 1 = 3x
- Diagonal 2 = 4x
The relationship between the sides and diagonals of a parallelogram is given by the formula:
d21+d22=2(a2+b2)
where d1 and d2 are the lengths of the diagonals, and a and b are the lengths of the sides.
Given that the sides of the parallelogram are 8 cm and 6 cm, we can substitute these values into the formula:
(3x)2+(4x)2=2(82+62)
Calculating the squares:
(3x)2=9x2
(4x)2=16x2
Thus, we have:
9x2+16x2=2(64+36)
Combine the left side:
25x2=2(100)
This simplifies to:
25x2=200
Now, divide both sides by 25:
x2=20025=8
Taking the square root gives:
x=√8=2√2
Now, we can find the lengths of the diagonals:
- Diagonal 1 = 3x=3(2√2)=6√2
- Diagonal 2 = 4x=4(2√2)=8√2
The difference between the lengths of the diagonals is:
Difference=8√2−6√2=2√2
The difference between the lengths of the diagonals is 2√2 cm.
Topper's Solved these Questions
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:Practice Exercises (EXPERT LEVEL)
Explore 45 Videos
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:TEST YOURSELF
Explore 15 Videos
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:Practice Exercises ( Foundation Level)
Explore 70 Videos
- LOGARITHMSBook:DISHA PUBLICATIONChapter:LOGARITHMSExercise:Test Yourself
Explore 15 Videos
- MOCK TEST - 3Book:DISHA PUBLICATIONChapter:MOCK TEST - 3Exercise:Multiple Choice Questions
Explore 20 Videos
Similar Questions
Knowledge Check
The sides of a parallelogram are 12 cm and 8 cm long and one of the diagonals is 10 cm long. If d is the length of other diagonal, then which one of the following is correct?
Ad<8cmB8cm<d<10cmC10cm<d<12cmDd>12cmTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
A40√3cm2B49√3cm2C48√6cm2D58√6cm2□ABCD is a parallelogram, AB=14cm,BC=18cmandAC=16cm. Find the length of the other diagonal:
A24 cmB28 cmC36 cmD32 cm
Sum of the squares of adjacent sides of a parallelogram is 130 cm length of one of its diagonals is 14 cm. Find the length of the other diagonal.
View SolutionSum of the squares of adjacent sides of a parallelogram is 130 sq. cm and length of one of its diagonals is 14 cm. Find the length of the other diagonal.
View SolutionThe adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm , and the diagonal ac measures 42 cm . Find the area of the parallelogram
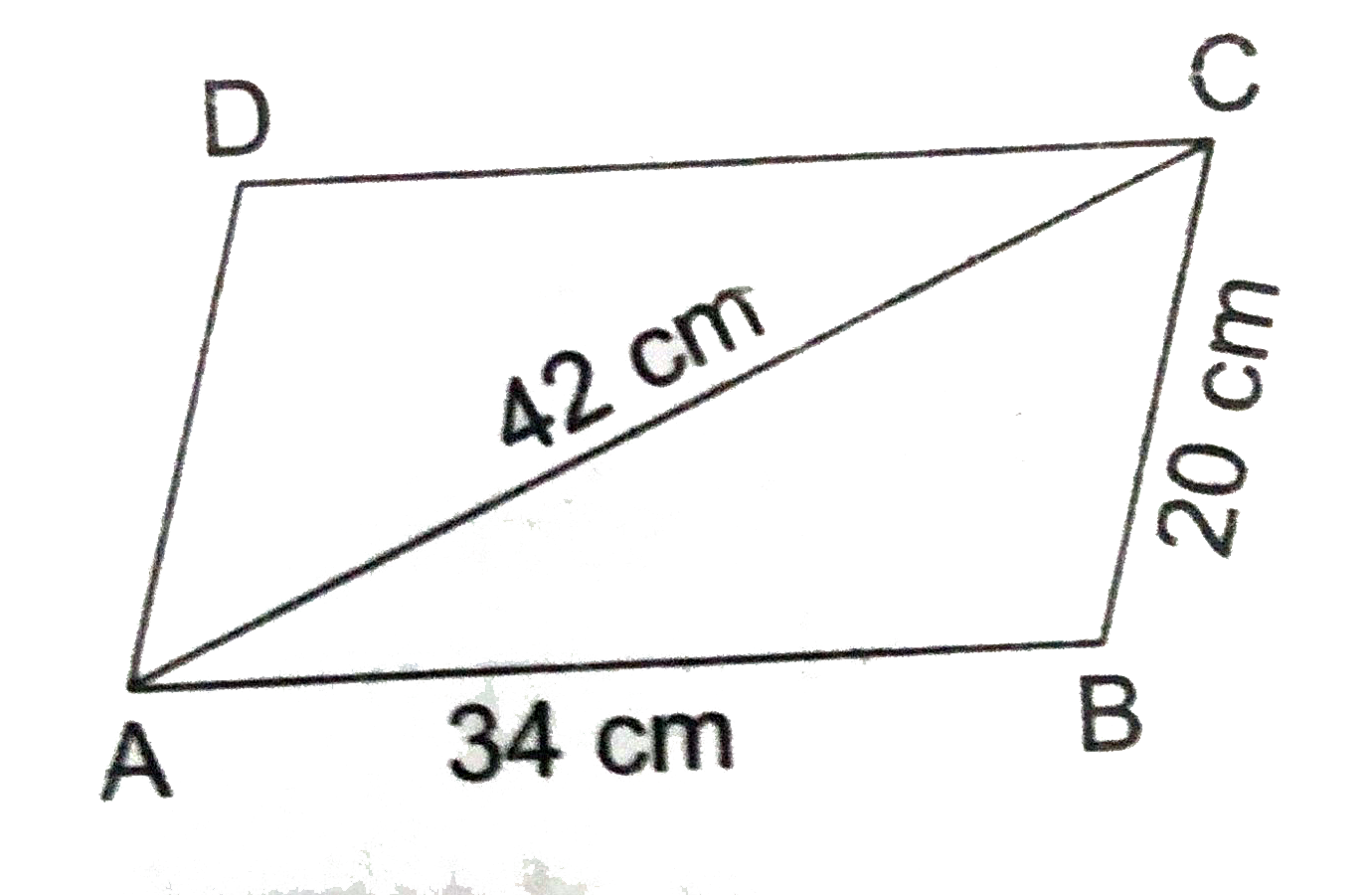
View SolutionThe adjacent sides of a parallelogram ABCD measure 34 cm and20 cm , and the diagonal AC measures 42 cm Find the area of the parallelogram.
View SolutionIf the parallel sides of a trapezium are 8 cm and 4 cm, M and N are the mid points of the diagonals of the trapezium, then length of MN is
View Solution
