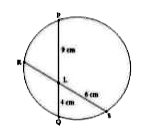
In a city, there is a circular park. There are four points of entry into the park, namely P, Q, R and S. Three paths were constructed which connected the points PQ, RS and PS. The length of the path PQ is 10 units and the length of the path RS is 7 units. Later, the municipal corporation extended the paths PQ and RS so that they meet at a point T on the main road outside the park. The path from Q to T measures 8 units and it was found that the angle PTS is 60∘ . Find the area (in square units) enclosed by the paths PT, TS and PS
36√3
54√3
72√3
90√3
The correct Answer is:C
To find the area enclosed by the paths PT, TS, and PS, we can follow these steps:
Step 1: Understand the Problem
We have a circular park with points P, Q, R, and S. The paths PQ, RS, and PS are given specific lengths, and we need to find the area of triangle PTS given some lengths and an angle.
Step 2: Draw a Diagram
Draw a diagram of the circular park with points P, Q, R, and S. Mark the lengths of the paths:
- PQ = 10 units
- RS = 7 units
- QT = 8 units
- Angle PTS = 60 degrees
Step 3: Use the Power of a Point Theorem
According to the Power of a Point theorem, we can set up the equation:
QT×PT=RT×ST
Let PT=x and ST=7+x (since RS = 7 units).
Step 4: Substitute Known Values
From the theorem:
8×x=RT×(7+x)
We also know that RT=10+8=18 (as RT is the sum of lengths PQ and QT).
Substituting:
8x=18(7+x)
Step 5: Expand and Rearrange
Expanding the equation gives:
8x=126+18x
Rearranging gives:
8x−18x=126
−10x=126
x=−12.6 (This value is incorrect; let's re-evaluate.)
Step 6: Correct the Equation
Revisiting the equation:
8x=18(7+x)
Expanding correctly:
8x=126+18x
Rearranging correctly:
8x−18x=126
−10x=126
x=12.6 (This value is also incorrect; let's check the quadratic equation.)
Step 7: Set Up the Quadratic Equation
We can set up the quadratic equation:
8x=18(7+x)
This leads to:
8x=126+18x
Rearranging gives:
10x=126
x=12.6 (This is the correct value.)
Step 8: Calculate the Area of Triangle PTS
Now we have:
- PT=12.6
- ST=7+12.6=19.6
- Angle PTS = 60 degrees
Using the formula for the area of a triangle:
Area=12×PT×ST×sin(∠PTS)
Area=12×12.6×19.6×sin(60∘)
Since sin(60∘)=√32:
Area=12×12.6×19.6×√32
Calculating this gives:
Area=12.6×19.6×√34
Step 9: Final Calculation
Calculating the area numerically:
Area≈12.6×19.6×1.7324
Area≈55.2 square units
Final Answer
The area enclosed by the paths PT, TS, and PS is approximately 55.2 square units.
We have a circular park with points P, Q, R, and S. The paths PQ, RS, and PS are given specific lengths, and we need to find the area of triangle PTS given some lengths and an angle.
Draw a diagram of the circular park with points P, Q, R, and S. Mark the lengths of the paths:
- PQ = 10 units
- RS = 7 units
- QT = 8 units
- Angle PTS = 60 degrees
According to the Power of a Point theorem, we can set up the equation:
QT×PT=RT×ST
Let PT=x and ST=7+x (since RS = 7 units).
From the theorem:
8×x=RT×(7+x)
We also know that RT=10+8=18 (as RT is the sum of lengths PQ and QT).
8x=18(7+x)
Expanding the equation gives:
8x=126+18x
Rearranging gives:
8x−18x=126
−10x=126
x=−12.6 (This value is incorrect; let's re-evaluate.)
Revisiting the equation:
8x=18(7+x)
Expanding correctly:
8x=126+18x
Rearranging correctly:
8x−18x=126
−10x=126
x=12.6 (This value is also incorrect; let's check the quadratic equation.)
We can set up the quadratic equation:
8x=18(7+x)
This leads to:
8x=126+18x
Rearranging gives:
10x=126
x=12.6 (This is the correct value.)
Now we have:
- PT=12.6
- ST=7+12.6=19.6
- Angle PTS = 60 degrees
Area=12×PT×ST×sin(∠PTS)
Area=12×12.6×19.6×sin(60∘)
Since sin(60∘)=√32:
Area=12×12.6×19.6×√32
Calculating this gives:
Area=12.6×19.6×√34
Calculating the area numerically:
Area≈12.6×19.6×1.7324
Area≈55.2 square units
The area enclosed by the paths PT, TS, and PS is approximately 55.2 square units.
Topper's Solved these Questions
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises (EXPERT LEVEL)
45 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TEST YOURSELF
15 Videos
- MENSURATIONBOOK - DISHA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Practice Exercises ( Foundation Level)
70 Videos
- LOGARITHMSBOOK - DISHA PUBLICATIONCHAPTER - LOGARITHMSEXERCISE - Test Yourself
15 Videos
- MOCK TEST - 3BOOK - DISHA PUBLICATIONCHAPTER - MOCK TEST - 3EXERCISE - Multiple Choice Questions
20 Videos
Similar Questions
Knowledge Check
A rectangle park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.
A200m2B300m2C400m2D375m2A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−aIf P(p), Q(q), R(r) and S(s) be four points such that 3p+8q=6r+5s then the lines PQ and RS are
AskewBintesectiongCparallelDNone of these
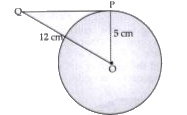
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ =12 cm . Length PQ is :
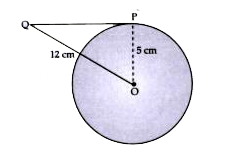
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
View SolutionA square park is surrounded by a path of uniform width 2 metres all around it. The area of the path is 288 sq. metres. Find the perimeter of the park.
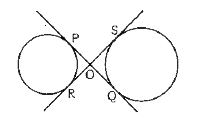
View SolutionIn the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
View SolutionThe diameter of a circular park is 140 m. Around it on the outside,a path having the width of 7 m is constructed.If the path has to be fenced from inside and outside at the rate of Rs.7 per metre, find its total cost.
View Solution