ABCD is a quadrilateral. The diagonals of ABCD intersect at the point P. The area of the triangles APD and BPC are 27 and 12, respectively. If the areas of the triangles APB and CPD are equal, then the area of triangle APB is
12
18
15
16
The correct Answer is:B
To find the area of triangle APB in the quadrilateral ABCD, we can use the information given about the areas of the triangles formed by the diagonals intersecting at point P.
1. Identify the Areas Given:
- Area of triangle APD = 27
- Area of triangle BPC = 12
- Let the area of triangle APB = x
- Since the areas of triangles APB and CPD are equal, we can denote the area of triangle CPD also as x.
2. Set Up the Area Relationship:
- The total area of quadrilateral ABCD can be expressed as:
\text{Area of ABCD} = \text{Area of APD} + \text{Area of BPC} + \text{Area of APB} + \text{Area of CPD
- Substituting the known values:
Area of ABCD=27+12+x+x=39+2x
3. Using the Property of Similar Triangles:
- Since triangles APB and CPD are equal in area and the triangles APD and BPC are given, we can use the ratio of the areas:
Area of APDArea of BPC=2712=94
- This ratio can also be expressed in terms of the areas of triangles APB and CPD:
xx=1
- Therefore, we can set up the equation based on the areas:
2712=xx
- This means that the areas of triangles APB and CPD are proportional to the areas of triangles APD and BPC.
4. Finding the Value of x:
- From the ratio of the areas, we can express:
2712=xx
- This does not provide new information since x cancels out. Instead, we can use the relationship derived from the total area:
- We know that the total area can also be expressed in terms of the areas of triangles APD and BPC:
Area of ABCD=Area of APD+Area of BPC+2x
- Setting the two expressions for the area of ABCD equal:
39+2x=27+12+2x
- Simplifying gives:
39+2x=39+2x
- This confirms our setup is correct.
5. Final Calculation:
- Since we know the areas of triangles APD and BPC, we can find x using the area ratios:
27+12=39
- The area of triangle APB can be calculated as:
x=√27×12=√324=18
Conclusion:
The area of triangle APB is 18.
- Area of triangle APD = 27
- Area of triangle BPC = 12
- Let the area of triangle APB = x
- Since the areas of triangles APB and CPD are equal, we can denote the area of triangle CPD also as x.
- The total area of quadrilateral ABCD can be expressed as:
\text{Area of ABCD} = \text{Area of APD} + \text{Area of BPC} + \text{Area of APB} + \text{Area of CPD
- Substituting the known values:
Area of ABCD=27+12+x+x=39+2x
- Since triangles APB and CPD are equal in area and the triangles APD and BPC are given, we can use the ratio of the areas:
Area of APDArea of BPC=2712=94
- This ratio can also be expressed in terms of the areas of triangles APB and CPD:
xx=1
- Therefore, we can set up the equation based on the areas:
2712=xx
- This means that the areas of triangles APB and CPD are proportional to the areas of triangles APD and BPC.
- From the ratio of the areas, we can express:
2712=xx
- This does not provide new information since x cancels out. Instead, we can use the relationship derived from the total area:
- We know that the total area can also be expressed in terms of the areas of triangles APD and BPC:
Area of ABCD=Area of APD+Area of BPC+2x
- Setting the two expressions for the area of ABCD equal:
39+2x=27+12+2x
- Simplifying gives:
39+2x=39+2x
- This confirms our setup is correct.
- Since we know the areas of triangles APD and BPC, we can find x using the area ratios:
27+12=39
- The area of triangle APB can be calculated as:
x=√27×12=√324=18
The area of triangle APB is 18.
Topper's Solved these Questions
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:Practice Exercises (EXPERT LEVEL)
Explore 45 Videos
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:TEST YOURSELF
Explore 15 Videos
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:Practice Exercises ( Foundation Level)
Explore 70 Videos
- LOGARITHMSBook:DISHA PUBLICATIONChapter:LOGARITHMSExercise:Test Yourself
Explore 15 Videos
- MOCK TEST - 3Book:DISHA PUBLICATIONChapter:MOCK TEST - 3Exercise:Multiple Choice Questions
Explore 20 Videos
Similar Questions
ABCD is a quadrilateral and its diagonals intersect at O.E,F,GandH are the midpoints of AO,BO,CO,andDO respectively. If the area of EFGH=50cm2, find the area of ABCD.
View SolutionThe diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the triangle CPD ?
View Solution
Knowledge Check
ABCD is a quadrilateral whose diagonals AC divides it into two parts, equal is area. Then, ABCD is
Aa rectangleBa ||gmCa rhombusDall of theseIn the adjoining figure , the ratio of the areas of the parallelogram ABCD and that of triangle ABN is :
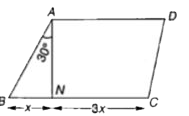 A6:1B5:1C4:1D8:1
A6:1B5:1C4:1D8:1
ABCD is a quadrilateral. The bisectors of angle A and B intersect at P, show that ∠C+∠D=2∠APB.
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionThe diagonals of quadrilateral ABCD, AC and BD intersects at O. Prove that if BO = OD then the triangles ABC and ADC are equal in area.
View SolutionCompute the area of quadrilateral ABCD.

View SolutionABCD is rectangle. P and Q are points on ABandBC respectively such that the area of triangle APD=5, area of triangle PBQ=4 and area of triangle QCD=3, all areas in square units. Then the areaof the triangle DPQ in square units is
View SolutionThe sides AD, BC of a trapezium. ABCD are parallel and the diagonals AC and BD meet at O. If the area of triangle AOB is 3 cm and the area of triangle BDC is 8 cm2, then what is the area of triangle AOD?
View Solution
