ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
3:7
3:8
3:5
4:9
The correct Answer is:B
Step by step video, text & image solution for ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and DeltaAEF by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, the area of parallelogram ABCD is
 AAB×BMBBC×BNCDC×DLDAD×DL
AAB×BMBBC×BNCDC×DLDAD×DLABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cmABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2
ABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View SolutionIf ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
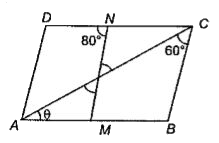
View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is

View Solution
