Find the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x?
A
3√3a232
B
3√3a216
C
34a2(π−12)
D
3a216
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for Find the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The area of a square ABCD is 36cm2. Find the area of the square obtained by joining the midpoints of the sides of the square ABCD.
A17 cm2B18 cm2C28 cm2D10 cm2The area of the circle that can be inscribed in a square of side 6 cm is
A36πcm2B18πcm2C12πcm2D9πcm2The area of a circle that can be inscribed in a square of side 6 cm is :
A36 πcm2B18 πcm2C12 πcm2D9 πcm2
The area of the circle that can be inscribed in a square of side 6 cm is
View SolutionWhat is the area of a circle inscribed in a square of side 'a' units?
View Solution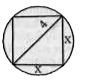
A square of side x is inscribed in a circle of radius 4 cm. Then x is
View SolutionWhat is the area of a circle which can be inscribed in a square of side 8 cm ?
View SolutionFind the ratio of the areas of squares circumscribed about and inscribed in the same circle.
View Solution
