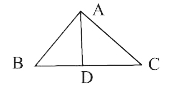
In , a line through a cuts the side BC at D such that BD : CD = 4: 5. If the area of , then the area of is
The correct Answer is:D
To solve the problem step by step, we will use the information provided in the question regarding the triangle ABC and the ratio of segments BD and CD.
1. Understanding the Ratio:
We are given that the ratio of BD to CD is 4:5. This means we can express BD and CD in terms of a common variable x:
- Let BD=4x
- Let CD=5x
2. Finding the Total Length of BC:
The total length of side BC can be calculated as:
BC=BD+CD=4x+5x=9x
3. Area of Triangle ABD:
We are given that the area of triangle ABD is 60cm2.
4. Using the Area Formula:
The area of triangle ABD can be expressed using the formula:
Area=12×Base×Height
Here, the base is BD=4x and the height from A to line BD is the same for both triangles ABD and ADC. Let’s denote this height as h. Therefore, we have:
60=12×4x×h
Simplifying this gives:
60=2xh⇒xh=30⇒h=30x
5. Finding the Area of Triangle ADC:
Now, we will find the area of triangle ADC. The base of triangle ADC is CD=5x and the height is still h. Thus, the area of triangle ADC can be calculated as:
Area of △ADC=12×CD×h=12×5x×h
Substituting h from the previous calculation:
Area of △ADC=12×5x×30x
Simplifying this gives:
Area of △ADC=12×5×30=1502=75cm2
Final Answer:
The area of triangle ADC is 75cm2.
---
We are given that the ratio of BD to CD is 4:5. This means we can express BD and CD in terms of a common variable x:
- Let BD=4x
- Let CD=5x
The total length of side BC can be calculated as:
BC=BD+CD=4x+5x=9x
We are given that the area of triangle ABD is 60cm2.
The area of triangle ABD can be expressed using the formula:
Area=12×Base×Height
Here, the base is BD=4x and the height from A to line BD is the same for both triangles ABD and ADC. Let’s denote this height as h. Therefore, we have:
60=12×4x×h
Simplifying this gives:
60=2xh⇒xh=30⇒h=30x
Now, we will find the area of triangle ADC. The base of triangle ADC is CD=5x and the height is still h. Thus, the area of triangle ADC can be calculated as:
Area of △ADC=12×CD×h=12×5x×h
Substituting h from the previous calculation:
Area of △ADC=12×5x×30x
Simplifying this gives:
Area of △ADC=12×5×30=1502=75cm2
The area of triangle ADC is 75cm2.
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - IV
Explore 169 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:Test Yourself
Explore 28 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
Knowledge Check
In ΔABC , a line through A cuts the side BC at D such that BD :DC =4 :5 if the area of ΔABD=60cm2 , then the area of ΔADC is
A90cm2B50cm2C60cm2D75cm2If ΔABC is similar to ΔDEF such that BC = 3 cm, EF = 4 cm and area of ΔABC=54cm2, then the area of ΔDEF is :
A66cm2B78cm2C96cm2D54cm2If D,E and F are respectively the midpoint of the sides BC,CA and AB of a ΔABC and the area of ΔABC=36cm2 , then area of ΔDEF is -----
A12cm2B9cm2C18cm2D8cm2
In a Δ ABC , D and E are two points on BC such that BD : DE : EC = 4 : 5 : 6 If the area of ΔADE=30cm2. find area of ΔABC
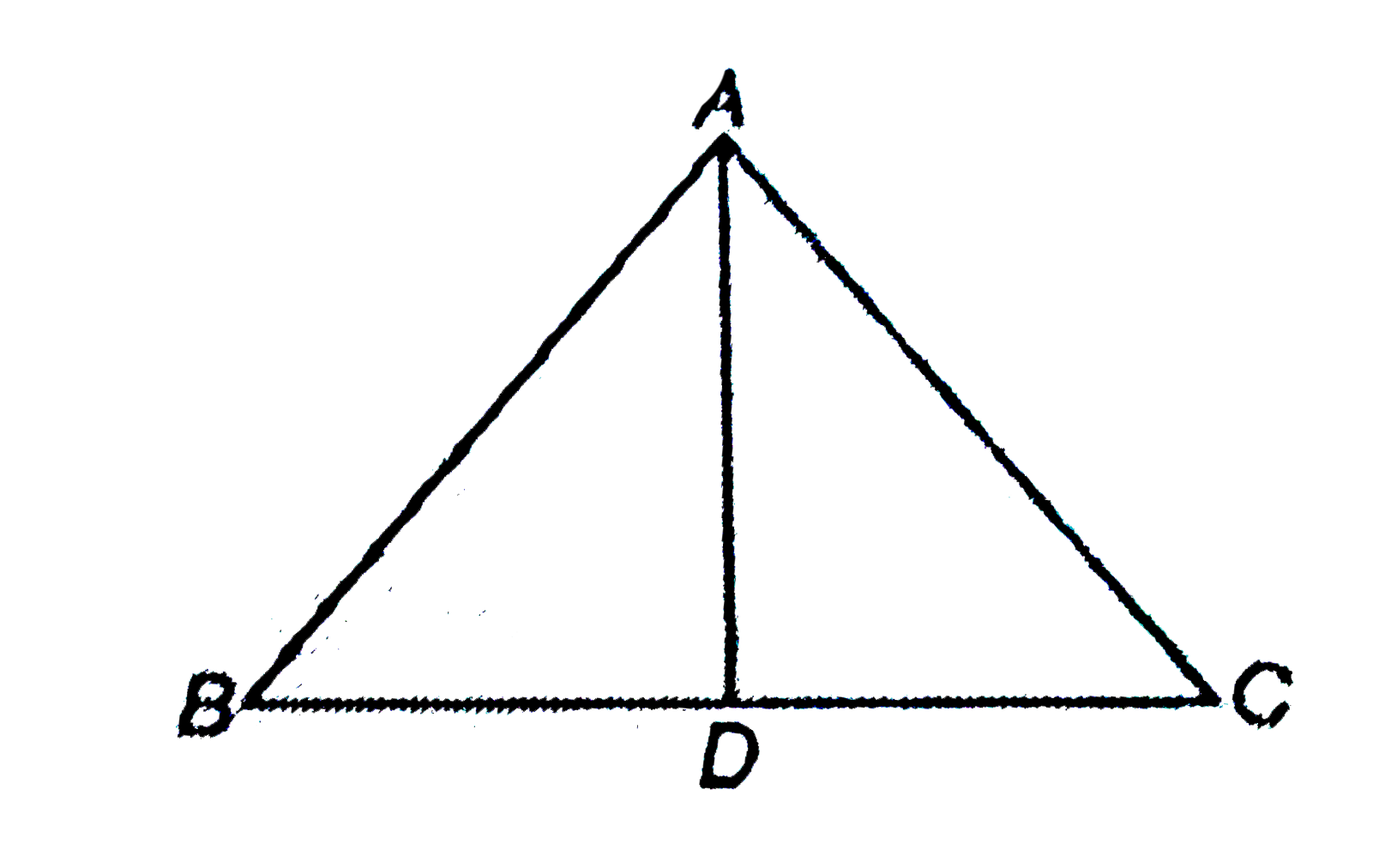
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
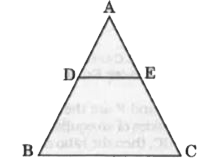
View SolutionIn figure, DE || BC. IF DE = 3 cm, BC = 6 cm and area of ΔADE=15 sq. cm, then the area of ΔABC is
View SolutionIn a Δ ABC , DE||BC if DE=23 BC and area of ΔABC =81cm2 find the area of ΔADE
View SolutionIn ΔABC,AB=6cm,BC=7cm and AC=5cm .The area of ΔABC is
View Solution