Question

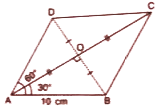
In a rhombus ABCD, $\angle A={60}^{\circ }$, AB = 12cm. Then the diagonal BD is

Options

A. 10 cm
B. `2sqrt(3) cm`
C. 6 cm
D. 12 cm

Answer

D

Explanation

To find the length of diagonal BD in rhombus ABCD, where angle A = 60° and side AB = 12 cm, we can follow these steps:

1. Understand the properties of a rhombus:
- In a rhombus, the diagonals bisect each other at right angles (90°).
- The opposite angles are equal.

2. Identify the angles:
- Given that angle A = 60°, angle B will also be 60° (since opposite angles are equal).
- Therefore, angle D = 60° and angle C = 120° (since the sum of angles in a quadrilateral is 360°).

3. Determine the angles at point O (the intersection of the diagonals):
- Since diagonals bisect each other at right angles, angle AOB = 90°.
- We can find angle AOB by splitting angle A into two equal parts: angle BAD = angle AOB = 30°.

4. Use triangle AOB:
- In triangle AOB, we know:
- AB = 12 cm (hypotenuse),
- Angle AOB = 90°,
- Angle OAB = 30°.
- We need to find OB (half of diagonal BD).

5. Apply trigonometric ratios:
- Using the sine function:
\( \sin(30°) = \frac{OB}{AB} \)
- We know that \(\sin(30°) = \frac{1}{2}\). Therefore:
\( \frac{1}{2} = \frac{OB}{12} \)
- Solving for OB:
\( OB = 12 \times \frac{1}{2} = 6 \text{ cm} \)

6. Calculate diagonal BD:
- Since O is the midpoint of diagonal BD, we have:
\( BD = 2 \times OB = 2 \times 6 = 12 \text{ cm} \)

Final Answer:
The length of diagonal BD is 12 cm.

---