If the perimeter of a semicircular field is 144m, then the diameter of the field is (take π=227)
55m
30 m
28 m
56m
The correct Answer is:D
To solve the problem, we need to find the diameter of a semicircular field given that its perimeter is 144 meters. We'll use the value of π as 227.
1. Understand the Perimeter of a Semicircle:
The perimeter P of a semicircular field can be calculated using the formula:
P=πr+2r
where r is the radius of the semicircle. The term πr represents the curved part, and 2r represents the two straight edges (the diameter).
2. Set Up the Equation:
Given that the perimeter is 144 meters, we can set up the equation:
πr+2r=144
3. Substitute the Value of π:
Substitute π with 227:
227r+2r=144
4. Combine the Terms:
To combine the terms, we need a common denominator. Rewrite 2r as 14r7:
22r7+14r7=144
This simplifies to:
36r7=144
5. Clear the Fraction:
Multiply both sides by 7 to eliminate the fraction:
36r=144×7
Calculate 144×7:
36r=1008
6. Solve for r:
Divide both sides by 36 to find r:
r=100836
Simplifying this gives:
r=28 meters
7. Calculate the Diameter:
The diameter d of the semicircle is given by:
d=2r
Substituting the value of r:
d=2×28=56 meters
Final Answer:
The diameter of the semicircular field is 56 meters.
---
The perimeter P of a semicircular field can be calculated using the formula:
P=πr+2r
where r is the radius of the semicircle. The term πr represents the curved part, and 2r represents the two straight edges (the diameter).
Given that the perimeter is 144 meters, we can set up the equation:
πr+2r=144
Substitute π with 227:
227r+2r=144
To combine the terms, we need a common denominator. Rewrite 2r as 14r7:
22r7+14r7=144
This simplifies to:
36r7=144
Multiply both sides by 7 to eliminate the fraction:
36r=144×7
Calculate 144×7:
36r=1008
Divide both sides by 36 to find r:
r=100836
Simplifying this gives:
r=28 meters
The diameter d of the semicircle is given by:
d=2r
Substituting the value of r:
d=2×28=56 meters
The diameter of the semicircular field is 56 meters.
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE -II
Explore 386 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
Knowledge Check
If the perimeter of a semicircular protractor is 36cm, find its diameter.
A12 cmB13 cmC14 cmD15 cmThe perimeter of a circular field is 242m. The area of the field is
A9317m2B18634m2C4658.5m2Dnone of theseThere is a rectangular tank of length 180 m and breadth 120 m in a circular field. If the area of the lad portion of the field is 40000m2, what is the radius of the field ? (Take π=227)
A130mB135mC140mD145m
If the perimeter of a semicircular protractor is 66 cm, find the diameter of the protractor (Take π=22/7)
View SolutionFind the perimeter of the given shape (Take π=227)
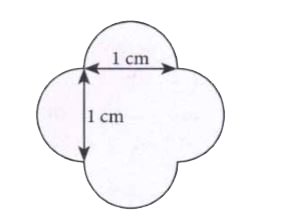
View SolutionIf the diameter of a semicircular protractor is 14 cm, then find its perimeter.
View SolutionIf the perimeter of a semicircular park is 360 m, then what is its area? (Take π=227)
View SolutionThe ratio between the area of a square and that of a circle, when the length of a side of the square is equal to that of the diameter of the circle, is
(Take, π=227)
View Solution
