The cliff a mountain is 180 m high and the angles of depression of two ships on the either side of cliff are 30∘and60∘ .What is the distance between the tow ships ?
400 metres
400√3 metre
145.68 metre
39.6metre
The correct Answer is:C
To solve the problem, we will use the concept of trigonometry, specifically the tangent function, which relates the angles of depression to the heights and distances involved.
1. Understand the Problem:
- We have a cliff (height = 180 m) and two ships on either side of the cliff.
- The angles of depression from the top of the cliff to the ships are 30° and 60°.
2. Draw a Diagram:
- Let point A be the top of the cliff, point D be the base of the cliff directly below A, and points B and C be the positions of the two ships.
- The height AD = 180 m.
- The angle of depression to ship B is 30° and to ship C is 60°.
3. Identify the Right Triangles:
- Triangle ABD for ship B and triangle ACD for ship C.
- In triangle ABD, angle ADB = 30°.
- In triangle ACD, angle ADC = 60°.
4. Calculate Distance BD (from A to B):
- Using the tangent function:
tan(30°)=ADBD
- Substituting the known values:
tan(30°)=180BD
- We know that tan(30°)=1√3:
1√3=180BD
- Rearranging gives:
BD=180√3
5. Calculate Distance CD (from A to C):
- Using the tangent function again:
tan(60°)=ADCD
- Substituting the known values:
tan(60°)=180CD
- We know that tan(60°)=√3:
√3=180CD
- Rearranging gives:
CD=180√3=60√3
6. Calculate the Distance Between the Two Ships (BC):
- The distance between the two ships is given by:
BC=BD+CD
- Substituting the values we found:
BC=180√3+60√3=240√3
7. Approximate the Distance:
- Using the approximate value of √3≈1.732:
BC≈240×1.732=415.68 m
Final Answer:
The distance between the two ships is approximately 415.68 meters.
- We have a cliff (height = 180 m) and two ships on either side of the cliff.
- The angles of depression from the top of the cliff to the ships are 30° and 60°.
- Let point A be the top of the cliff, point D be the base of the cliff directly below A, and points B and C be the positions of the two ships.
- The height AD = 180 m.
- The angle of depression to ship B is 30° and to ship C is 60°.
- Triangle ABD for ship B and triangle ACD for ship C.
- In triangle ABD, angle ADB = 30°.
- In triangle ACD, angle ADC = 60°.
- Using the tangent function:
tan(30°)=ADBD
- Substituting the known values:
tan(30°)=180BD
- We know that tan(30°)=1√3:
1√3=180BD
- Rearranging gives:
BD=180√3
- Using the tangent function again:
tan(60°)=ADCD
- Substituting the known values:
tan(60°)=180CD
- We know that tan(60°)=√3:
√3=180CD
- Rearranging gives:
CD=180√3=60√3
- The distance between the two ships is given by:
BC=BD+CD
- Substituting the values we found:
BC=180√3+60√3=240√3
- Using the approximate value of √3≈1.732:
BC≈240×1.732=415.68 m
The distance between the two ships is approximately 415.68 meters.
Topper's Solved these Questions
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -V
45 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TEST YOURSELF
25 Videos
- TRIGONOMETRY BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -III
90 Videos
- TIME AND WORKBOOK - KIRAN PUBLICATIONCHAPTER - TIME AND WORKEXERCISE - TEST YOURSELF
25 Videos
Similar Questions
From the top of 120 m high lighthouse, the angle of depression of two ships on opposite side of the base of the lighthouse is 30∘ and 60∘. What is the distance between the ships? (rounded off)
120 मी ऊँची लाइट हाउस के शीर्ष से इसके आधार के विपरीत दिशाओं में दो जहाज़ो का अवनमन कोण 30∘ और 60∘ है | जहाज़ों के बीच की दूरी ज्ञात करें |
View SolutionA man on the top of a cliff 100 meter high, observes the angles of depression of two points on the opposite sides of the cliff as 30∘ and 60∘ respectively. Find the difference between the two points.
View Solution
Knowledge Check
From the top of a tower of height 180 m the angles of depression of two objects on either sides of the tower are 30∘and45∘ . Then the distance between the objects are
A180(3+√3)mB180(3−√3)mC180(√3−1)mD180(√3+1)mTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
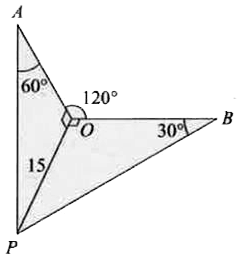 A5√39 mB5√30 mC5√21 mD5√3 m
A5√39 mB5√30 mC5√21 mD5√3 mFrom the top of a lighthouse. 100 m high, the angle of depression of two ships are 30° and 45°, if both ships are on same side find the distance between the ships ?
AA. 120 mBB. 180 mCC. 240 mDD. 360 m
The angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and tower.
View SolutionTwo ships are sailing in the sea on the either side of the lighthouse.The angles of depression of two ships as observed from the top of the lighthouse are 60∘ and 45∘, respectively. If the distance between the ships is 100(√3+1√3) m, then find the height of the lighthouse
View SolutionTwo men on either side of a temple 126 m high observe the angle of elevation of the top of the temple to be 30∘and60∘ respectively. Find the distance between the two men ?
View SolutionAs observed from the top of a light house the angle of depression of two ships in opposite direction are respectively 60∘and45∘. If distance between the two ships in 200(√3+1√3) meter then find the height of the light house.
View SolutionA helicopter, at an altitude of 1500 metre, finds that two ships are sailing towards it, in the same direction. The angles of depression of the ships as observed from the helicopter are 60∘and30∘ respectively. Distance between the two ships, in metre is
View Solution
