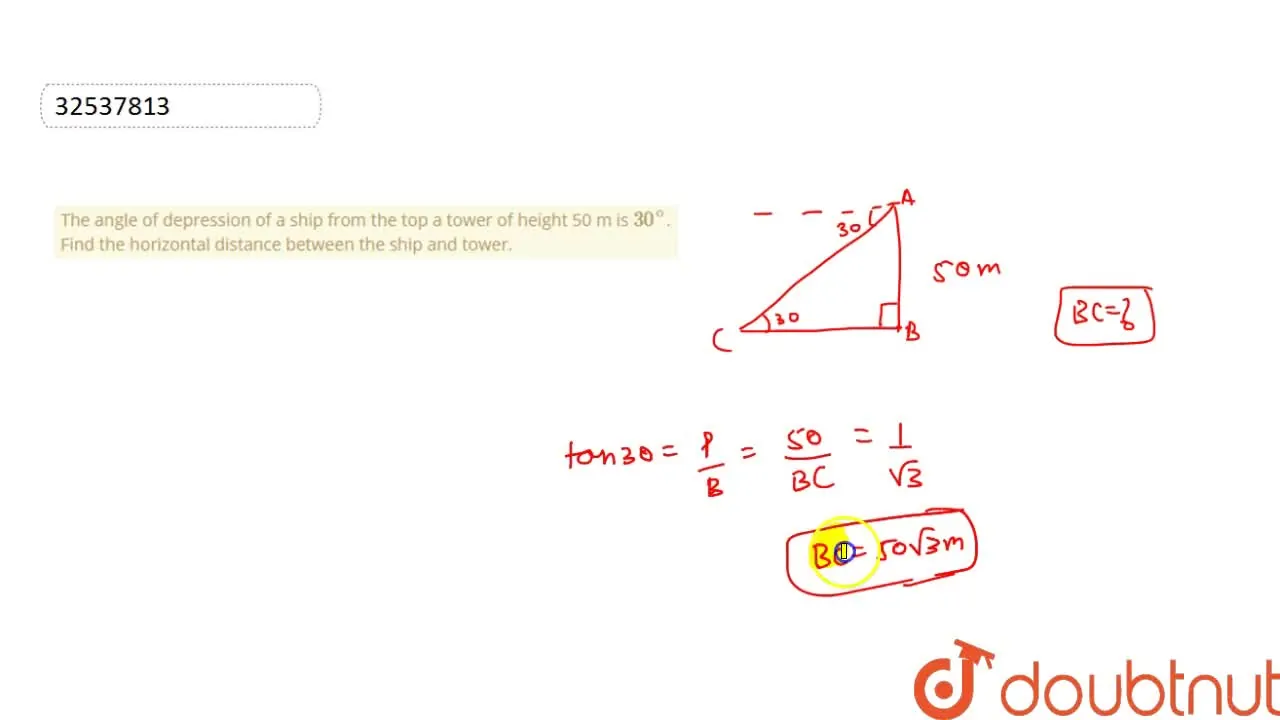
The angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and tower.
The correct Answer is:50√3m
Step by step video, text & image solution for The angle of depression of a ship from the top a tower of height 50 m is 30^(@). Find the horizontal distance between the ship and tower. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (long Answer Questions)1videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions5videos
REAL NUMBERS
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
Similar Questions
The angle if depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the boat and the bridge.
View SolutionThe height of a light house is 40 m. The angle of depression of a ship from the top of the light house is 60∘. Find the distance of ship from the light house.
View SolutionThe angle of depression of 47 m high building form the top of a tower 137 m high is 30∘ . Calculate the distance between the building and the tower .
View SolutionThe angle of depression between a flying kite and 'a' point on the ground is 60 m. If the string makes 30∘. Find the horizontal distance between the ship and tower.
View SolutionThe angle of depression of a ship from the top of a 30 m hight tower is 60∘. The distance of ship from the base of the tower is
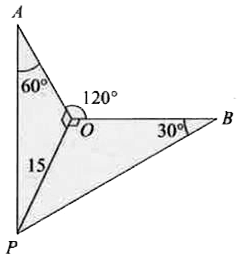
View SolutionTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
 View Solution
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also the height of the other tower.
View SolutionFrom the top of a platform, the angle of elevation of a tower was 30∘. The tower was 45 m high and the horizontal distance between the platform and the tower was 40√3 m. What was the height of the platform?
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two and also the height of the tower.
View SolutionThe angle of depression of the foot of a building from the top of a tower 30 m away is 30∘. How high is the tower?
View Solution