In the adjoining figure, the length of BC is
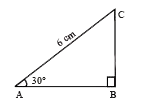
(a)2√3 cm
(b)3√3 cm
(c)4√3 cm
(d)3 cm
2√3 cm
3√3 cm
4√3 cm
3 cm
The correct Answer is:D
Step by step video, text & image solution for In the adjoining figure, the length of BC is (a)2sqrt3 cm (b)3sqrt3 cm (c)4sqrt3 cm (d)3 cm by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the surface area of a cube is 13254 cm2, then the length of its diagonal is 44√3cm (b) 45√3cm (c) 46√3cm (d) 47√3cm
View SolutionTwo tangents making an angle of 1200 with each other are drawn to a circle of radius 6cm, then the length of each tangent is equal to √3 cm (b) 6 √3 cm (c) √2 cm (d) 2 √3 cm
View Solution
Knowledge Check
Three circles of radius 1 cm are circumscribed by a circle of radius r, as shown in the figure. Find the value of r?
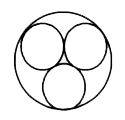
(a)√3+1
(b)2+√3√3
(c)√3+2√2
(d)2+√3A√3+1B2+√3√3C√3+2√2D2+√3If the perimeter of a rhombus is 56 cm and the length of one of its diagonals is 26 cm. then find the length of the other diagonal of the rhombus.
A)6√7 cm
B)6√5 cm
C)6√3 cm
D)6√2 cmA6√7 cmB6√5 cmC6√3 cmD6√2 cm
If slant height of a right circular cone is 3cm then the maximum volume of cone is (a) 2√3πcm3 (b) 4√3πcm3 (c) (2+√3)πcm3 (d) (2−√3)πcm3
View SolutionIn the given figure (not to scale), PQ is a tangent segment , drawn to the circle with centre O at P and QR =RO. iF PQ=3√3cm, and ORQ is a line segment, then find the radius of the circle.
(a) √3cm
(b) 3cm
(c) 2√3cm
(d) 2cm

View SolutionThe area of an equilateral triangle is 4√3 cm2. The length of each of its side is (a)3 cm (b) 4 cm (c)2√3 cm (d) √32 cm
View SolutionWhat is the area of △PQR, shown in Fig.? (a) 2√154 sq. cm (b) 3√154 sq. cm (c) 4√308 sq. cm (d) Cannot be determined (e) None of these
View SolutionIf the total length of diagonals of a cube is 12 cm, then what is the total length of the edges of the cube? 6√3cm (b) 12cm (c) 15cm (d) 12√3cm
View SolutionA circle is inscribed in a square. An equilateral triangle of side 4√3 cm is inscribed in that circle. The length of the diagonal of the square is 4√2cm (b) 8 cm (c) 8√2cm (d) 16 cm
View Solution
