Question

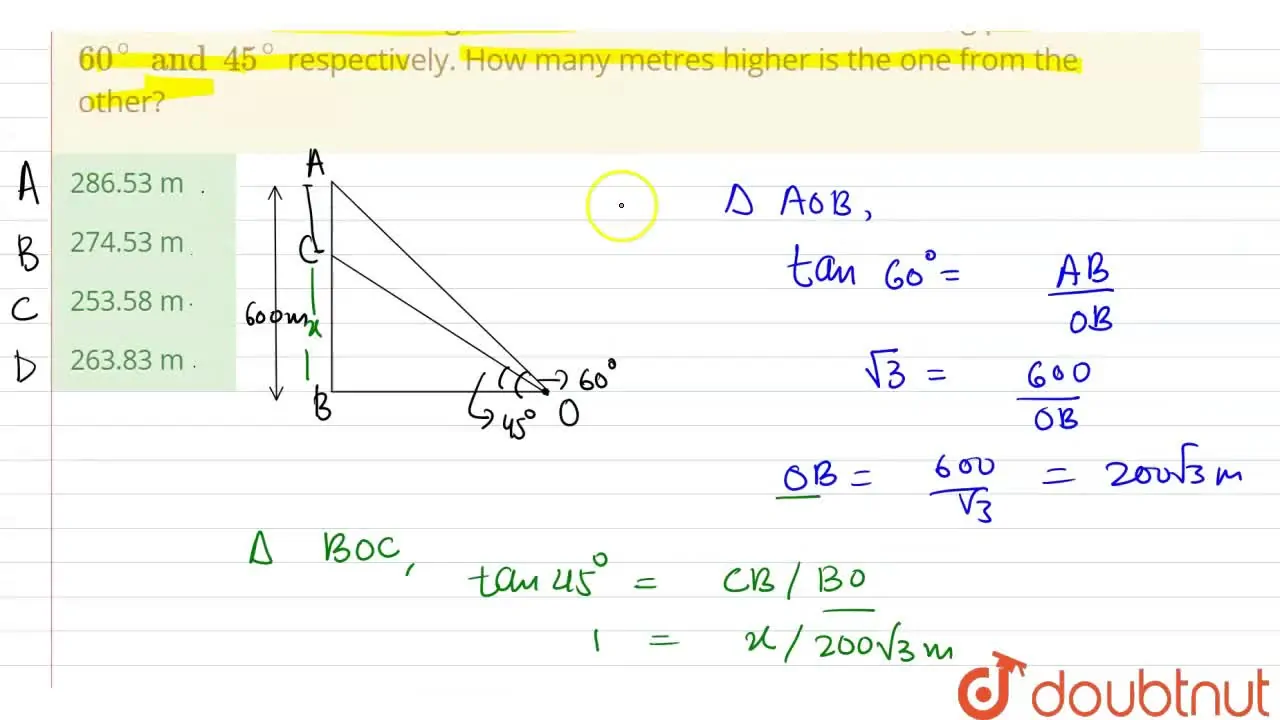
An aeroplane at a height of 600 m passes vertically above another aeroplane at an instant when their angles of elevation at the same observing point are ${60}^{\circ }\text{and}{45}^{\circ }$ respectively. How many metres higher is the one from the other?

Options

A. 286.53 m
B. 274.53 m
C. 253.58 m
D. 263.83 m

Answer

C

Explanation

To solve the problem step by step, we will use trigonometric ratios and properties of right triangles.

Step 1: Understand the Problem
We have two airplanes. The first airplane is at a height of 600 m, and the second airplane is below it. The angles of elevation from a point on the ground to the two airplanes are 60° and 45°, respectively. We need to find the height difference between the two airplanes.

Step 2: Draw a Diagram
Let's denote:
- Point O: the observer's position on the ground.
- Point A: the position of the first airplane (height = 600 m).
- Point B: the position of the second airplane.
- Point C: the point directly below the first airplane on the ground.

Step 3: Set Up the First Triangle (for the airplane at 600 m)
In triangle OAC (where A is the first airplane):
- Angle AOB = 60°
- Height OA = 600 m

Using the tangent function:
\( \tan(60^\circ) = \frac{OA}{OC} \)
\( \sqrt{3} = \frac{600}{OC} \)
From this, we can find OC:
\( OC = \frac{600}{\sqrt{3}} = 200\sqrt{3} \text{ m} \)

Step 4: Set Up the Second Triangle (for the airplane below)
In triangle OBC (where B is the second airplane):
- Angle BOC = 45°

Using the tangent function:
\( \tan(45^\circ) = \frac{OB}{OC} \)
Since \(\tan(45^\circ) = 1\):
\( 1 = \frac{OB}{OC} \)
Thus, \(OB = OC\).

Step 5: Calculate the Height of the Second Airplane
From the previous step, we know:
\( OB = OC = 200\sqrt{3} \text{ m} \)

Step 6: Find the Height of the Second Airplane (CB)
The height of the second airplane (CB) can be found using the relationship:
\( CB = OA - OB \)
Substituting the values:
\( CB = 600 - 200\sqrt{3} \)

Step 7: Calculate the Height Difference
Now, we need to find the height difference between the two airplanes:
\( \text{Height Difference} = OA - CB \)
Substituting the values:
\( \text{Height Difference} = 600 - (600 - 200\sqrt{3}) = 200\sqrt{3} \)

Step 8: Calculate the Numerical Value
Using the approximate value of \(\sqrt{3} \approx 1.732\):
\( 200\sqrt{3} \approx 200 \times 1.732 \approx 346.4 \text{ m} \)

Step 9: Final Calculation
Now we can find the height difference:
\( \text{Height Difference} = 600 - (600 - 200\sqrt{3}) = 200\sqrt{3} \approx 346.4 \text{ m} \)

Conclusion
The height difference between the two airplanes is approximately 346.4 m.