Find the area of the quadrilateral formed by the solution set of the inequations 2x+3y≤12,x0,y≥0 and x≤3.
6
8
9
12
The correct Answer is:C
To find the area of the quadrilateral formed by the solution set of the inequalities 2x+3y≤12, x≥0, y≥0, and x≤3, we will follow these steps:
Step 1: Graph the inequalities
1. Graph the line 2x+3y=12:
- To find the intercepts, set x=0:
3y=12⟹y=4(y-intercept)
- Now set y=0:
2x=12⟹x=6(x-intercept)
- The line intersects the axes at points (0,4) and (6,0).
2. Identify the bounded region:
- Since x≥0 and y≥0, we are only interested in the first quadrant.
- The line x=3 is a vertical line that intersects the x-axis at (3,0).
Step 2: Find the vertices of the quadrilateral
1. Vertices:
- The vertices of the quadrilateral are:
- O(0,0) (origin)
- A(0,4) (y-intercept)
- B(3,2) (intersection of the line 2x+3y=12 and x=3)
- C(3,0) (intersection of the line x=3 and the x-axis)
Step 3: Calculate the area of the quadrilateral
1. Area of quadrilateral OABC:
- The quadrilateral can be divided into a rectangle OACB and triangle OAB.
- Area of rectangle OACB:
- Width = 3 (from O to C)
- Height = 4 (from O to A)
Arearectangle=width×height=3×4=12 square units
2. Area of triangle OAB:
- Base = 3 (from O to B)
- Height = 2 (from B to the line y=0)
Areatriangle=12×base×height=12×3×2=3 square units
3. Total Area:
Total Area=Arearectangle+Areatriangle=12+3=15 square units
Final Answer
The area of the quadrilateral formed by the solution set of the inequalities is 15 square units.
1. Graph the line 2x+3y=12:
- To find the intercepts, set x=0:
3y=12⟹y=4(y-intercept)
- Now set y=0:
2x=12⟹x=6(x-intercept)
- The line intersects the axes at points (0,4) and (6,0).
- Since x≥0 and y≥0, we are only interested in the first quadrant.
- The line x=3 is a vertical line that intersects the x-axis at (3,0).
1. Vertices:
- The vertices of the quadrilateral are:
- O(0,0) (origin)
- A(0,4) (y-intercept)
- B(3,2) (intersection of the line 2x+3y=12 and x=3)
- C(3,0) (intersection of the line x=3 and the x-axis)
1. Area of quadrilateral OABC:
- The quadrilateral can be divided into a rectangle OACB and triangle OAB.
- Area of rectangle OACB:
- Width = 3 (from O to C)
- Height = 4 (from O to A)
Arearectangle=width×height=3×4=12 square units
- Base = 3 (from O to B)
- Height = 2 (from B to the line y=0)
Areatriangle=12×base×height=12×3×2=3 square units
Total Area=Arearectangle+Areatriangle=12+3=15 square units
The area of the quadrilateral formed by the solution set of the inequalities is 15 square units.
Topper's Solved these Questions
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Practice Exercises (Expert Level)
Explore 11 Videos
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Test Yourself
Explore 15 Videos
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Practice Exercises (Foundation Level)
Explore 14 Videos
- GEOMETRY Book:DISHA PUBLICATIONChapter:GEOMETRY Exercise:TEST YOURSELF
Explore 3 Videos
- INTERESTBook:DISHA PUBLICATIONChapter:INTERESTExercise:Test Yourself
Explore 15 Videos
Similar Questions
Knowledge Check
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A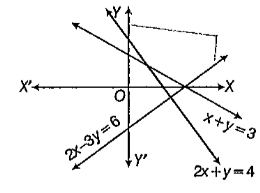 B
B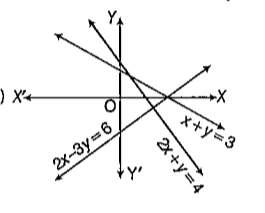 C
C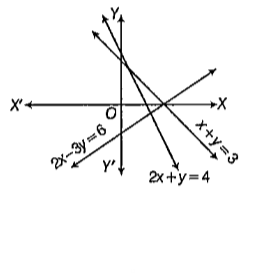 D
D
The solution set of
x−2y≥0,2x−y≤−2,x≥0,y≥0 isAEmptyBBoundedCNeither empty nor boundedDNone of theseThe solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
A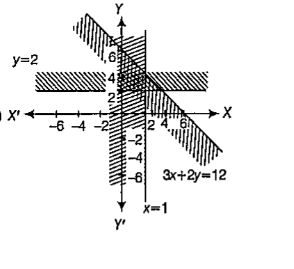 B
B C
C DNone of the above
DNone of the above
Find the solutions set of inequalities 0≤x≤5,0≤2y≤7
View SolutionGraph the solution sets of the following inequations:
y−2≤3x
View SolutionSolution set for inequality 2x−6≤0 is (0, 3].
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View SolutionMaximize 5x+7y, subject to the constraints 2x+3y≤12,x+y≤5,x≥0andy≥0.
View Solution
