Find the solutions set of inequalities 0≤x≤5,0≤2y≤7
The correct Answer is:z has minimum value 5 when x =0 y=5
To find the solution set of the inequalities 0≤x≤5 and 0≤2y≤7, we will follow these steps:
Step 1: Understand the inequalities
The inequalities can be broken down as follows:
1. 0≤x≤5 indicates that x can take any value from 0 to 5, inclusive.
2. 0≤2y≤7 can be simplified by dividing the entire inequality by 2, giving us 0≤y≤72.
Step 2: Graph the inequalities
To visualize the solution set, we will graph the inequalities on a coordinate plane.
1. Graph x=0 and x=5:
- The line x=0 is the y-axis.
- The line x=5 is a vertical line parallel to the y-axis at x=5.
2. Graph y=0 and y=72:
- The line y=0 is the x-axis.
- The line y=72 is a horizontal line parallel to the x-axis at y=3.5.
Step 3: Identify the feasible region
The feasible region is where all the inequalities overlap:
- The region where x is between 0 and 5 (including the boundaries).
- The region where y is between 0 and 72 (including the boundaries).
Step 4: Determine the vertices of the feasible region
The vertices of the rectangle formed by the intersection of these inequalities are:
1. (0,0)
2. (5,0)
3. (5,72)
4. (0,72)
Step 5: Conclusion
The solution set of the inequalities is the rectangular area defined by the vertices mentioned above, including the boundaries. Therefore, the solution set can be expressed as:
{(x,y)∣0≤x≤5 and 0≤y≤72}
The inequalities can be broken down as follows:
1. 0≤x≤5 indicates that x can take any value from 0 to 5, inclusive.
2. 0≤2y≤7 can be simplified by dividing the entire inequality by 2, giving us 0≤y≤72.
To visualize the solution set, we will graph the inequalities on a coordinate plane.
- The line x=0 is the y-axis.
- The line x=5 is a vertical line parallel to the y-axis at x=5.
- The line y=0 is the x-axis.
- The line y=72 is a horizontal line parallel to the x-axis at y=3.5.
The feasible region is where all the inequalities overlap:
- The region where x is between 0 and 5 (including the boundaries).
- The region where y is between 0 and 72 (including the boundaries).
The vertices of the rectangle formed by the intersection of these inequalities are:
1. (0,0)
2. (5,0)
3. (5,72)
4. (0,72)
The solution set of the inequalities is the rectangular area defined by the vertices mentioned above, including the boundaries. Therefore, the solution set can be expressed as:
{(x,y)∣0≤x≤5 and 0≤y≤72}
Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:DIFFERENTIATION
Explore 42 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:APPLICATIONS OF DERIVATIVE
Explore 44 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:LINE AND PLANE
Explore 40 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
Knowledge Check
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A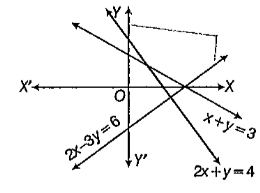 B
B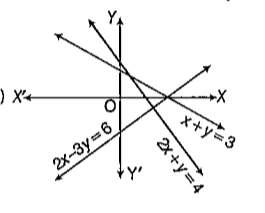 C
C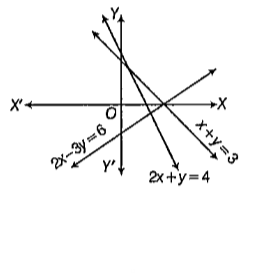 D
D
Find the solution set of −3x+2≤5and2x−5≤7.
A−1≤x≤−6B1≤x≤6C1≤x≤6D−1≤x≤6Find the area of the quadrilateral formed by the solution set of the inequations 2x+3y≤12,x0,y≥0 and x≤3.
A6B8C9D12
Solution set of the inequalities x+2y≥11,3x+4y≤30,2x+5y≤30,x≥0,y≥0 includes the point
View SolutionThe solution set of −5x+25≤0 is
View SolutionSolution set for inequality |x−1|≤5is.
View SolutionThe solution set of the inequation 15+3x≤0 is
View SolutionThe region represented by the solution set of the system of inequalities x−y≤1,x+2y≤8,2x+y≥2,0,y≥0is
View Solution

