Which of the following shaded regions shows the graph of the inequality y≤|x+2| ?
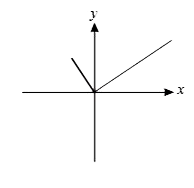
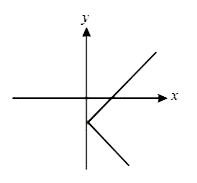

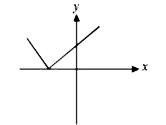
The correct Answer is:D
To solve the inequality y≤|x+2|, we need to break it down into two separate inequalities based on the definition of absolute value.
1. Understanding the Absolute Value:
The expression |x+2| can be rewritten as two separate cases:
- Case 1: x+2 when x+2≥0 (or x≥−2)
- Case 2: −(x+2) when x+2<0 (or x<−2)
2. Formulating the Inequalities:
From the two cases, we can derive the following inequalities:
- For Case 1: y≤x+2
- For Case 2: y≤−x−2
3. Finding the Points for Graphing:
- For the first inequality y=x+2:
- When x=0, y=0+2=2 → Point (0, 2)
- When y=0, 0=x+2 → x=−2 → Point (-2, 0)
- For the second inequality y=−x−2:
- When x=0, y=−0−2=−2 → Point (0, -2)
- When y=0, 0=−x−2 → x=−2 → Point (-2, 0)
4. Plotting the Points:
- On a Cartesian plane, plot the points (0, 2), (-2, 0) for the line y=x+2 and (0, -2), (-2, 0) for the line y=−x−2.
5. Drawing the Lines:
- Draw the line for y=x+2 and shade below it since the inequality is y≤x+2.
- Draw the line for y=−x−2 and shade below it since the inequality is y≤−x−2.
6. Identifying the Shaded Region:
- The solution to the inequality y≤|x+2| will be the region that is below both lines.
7. Choosing the Correct Option:
- Compare the shaded regions in the provided options (A, B, C, D) and identify which one matches the region below both lines.
Conclusion:
After analyzing the options, we find that option D correctly represents the shaded region that satisfies the inequality y≤|x+2|.
---
The expression |x+2| can be rewritten as two separate cases:
- Case 1: x+2 when x+2≥0 (or x≥−2)
- Case 2: −(x+2) when x+2<0 (or x<−2)
From the two cases, we can derive the following inequalities:
- For Case 1: y≤x+2
- For Case 2: y≤−x−2
- For the first inequality y=x+2:
- When x=0, y=0+2=2 → Point (0, 2)
- When y=0, 0=x+2 → x=−2 → Point (-2, 0)
- When x=0, y=−0−2=−2 → Point (0, -2)
- When y=0, 0=−x−2 → x=−2 → Point (-2, 0)
- On a Cartesian plane, plot the points (0, 2), (-2, 0) for the line y=x+2 and (0, -2), (-2, 0) for the line y=−x−2.
- Draw the line for y=x+2 and shade below it since the inequality is y≤x+2.
- Draw the line for y=−x−2 and shade below it since the inequality is y≤−x−2.
- The solution to the inequality y≤|x+2| will be the region that is below both lines.
- Compare the shaded regions in the provided options (A, B, C, D) and identify which one matches the region below both lines.
After analyzing the options, we find that option D correctly represents the shaded region that satisfies the inequality y≤|x+2|.
Topper's Solved these Questions
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Practice Exercises (Expert Level)
Explore 11 Videos
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Test Yourself
Explore 15 Videos
- INEQUALITIESBook:DISHA PUBLICATIONChapter:INEQUALITIESExercise:Practice Exercises (Foundation Level)
Explore 14 Videos
- GEOMETRY Book:DISHA PUBLICATIONChapter:GEOMETRY Exercise:TEST YOURSELF
Explore 3 Videos
- INTERESTBook:DISHA PUBLICATIONChapter:INTERESTExercise:Test Yourself
Explore 15 Videos
Similar Questions
Knowledge Check
The graph of the inequality 4x+6y≤24 is :
Ahalf plane that contains the origin, including the points on the line 4x+6y=24.Bhalf plane that does not contain the origin.Centire XOY plane.Dhalf plane that contains the origin.The graph of inequality 3x+y≤3 is:
Aclosed half plane that contains the origin.Bopen half plane that contains the origin.Copen half plane not containing the origin.Dclosed half plane not containing the origin.The shaded region is represented by the inequality:
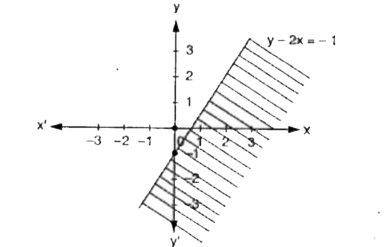 Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Which of the following inequations represents the shaded region?
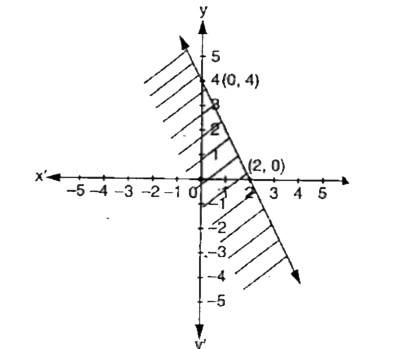
View SolutionThe shaded region for the inequality x+5y≤6 is
View SolutionThe shaded region is represented by the inequation:
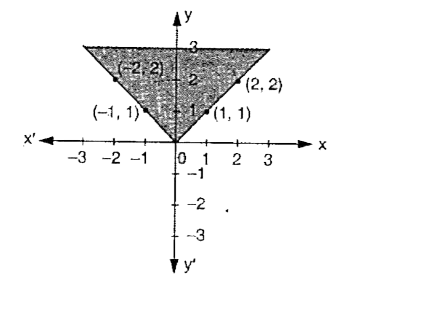
View SolutionThe shaded region for the inequality x+5y≤6 is
View SolutionWhich shows the solution to the inequality −3.5x−12≤58?
View Solution
