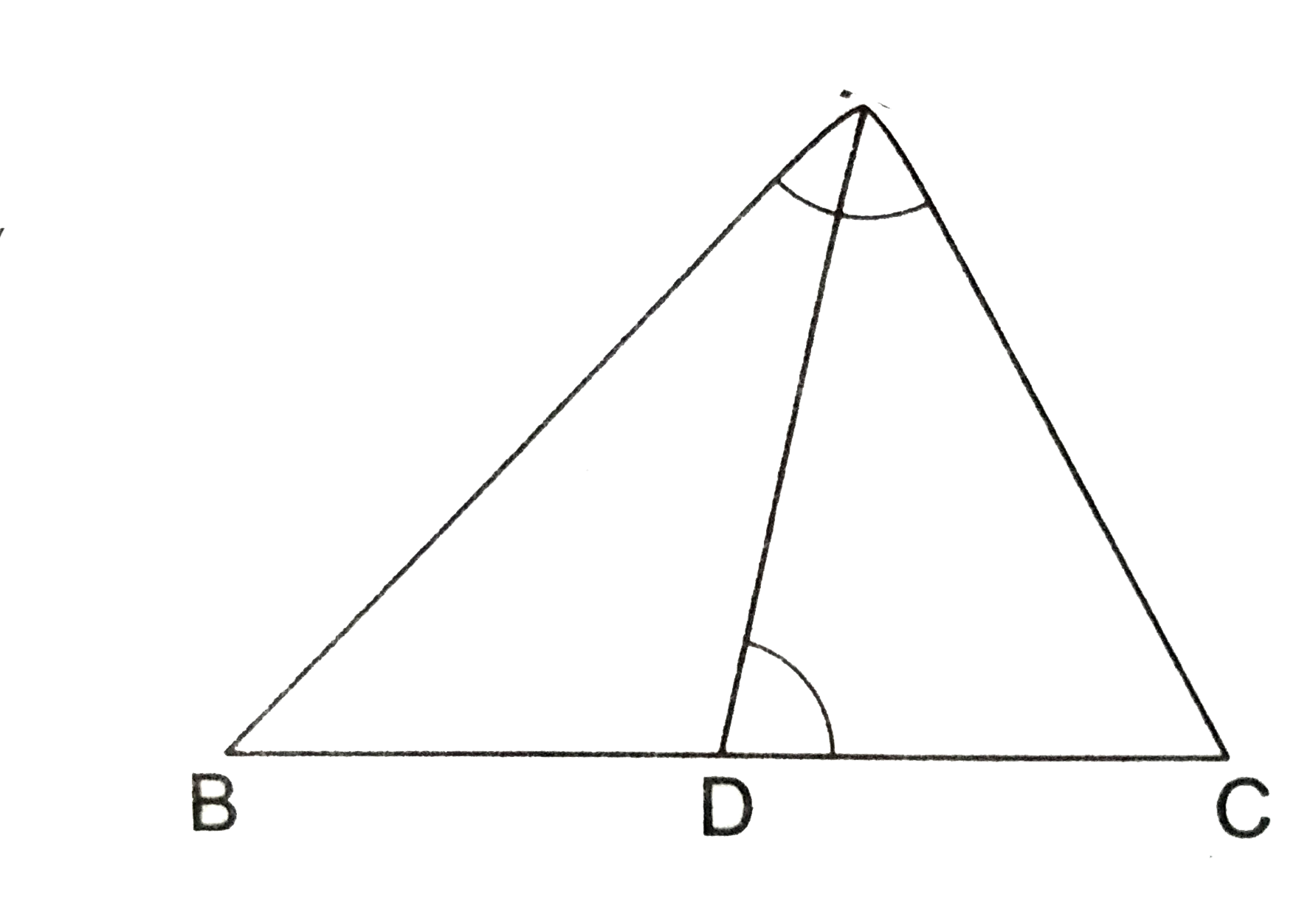
Assertion : In the given fig ure, the point D divides the side BC of △ABC in the ratio m:n, then ratio of ar(ABD) and ar(ADC) is m:n
Reason : Area of triangle = 1/2 × Base × Height
If both assertion and reason are tme and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is trne.
The correct Answer is:A
Step by step video, text & image solution for Assertion : In the given fig ure, the point D divides the side BC of /_\ABC in the ratio m : n, then ratio of ar(ABD) and ar(ADC) is m:n Reason : Area of triangle = 1/2 xx Base xx Height by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Comprehension Type )
6 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Very Short Answer Type )
9 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )
2 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
Knowledge Check
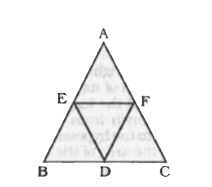
ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determinedABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determindIn △ABC, D divides BC in the ratio l:m, G divides AD in the ratio (l+m):n then the position vector of G is
Am¯c+n¯b+l¯am+n+lBl¯a+m¯b+n¯cm+n+lCn¯c+l¯b+m¯am+n+lDl¯c+m¯b+n¯am+n+l
If D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionIn ΔABCAD divides BC in 1 : 3 find the ratio of triangle ADB and ADC ?
View SolutionIn Fig. 9.29 ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of triangle ACD.
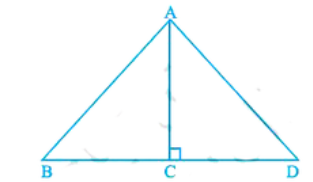
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View SolutionIn the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
View Solution