Question

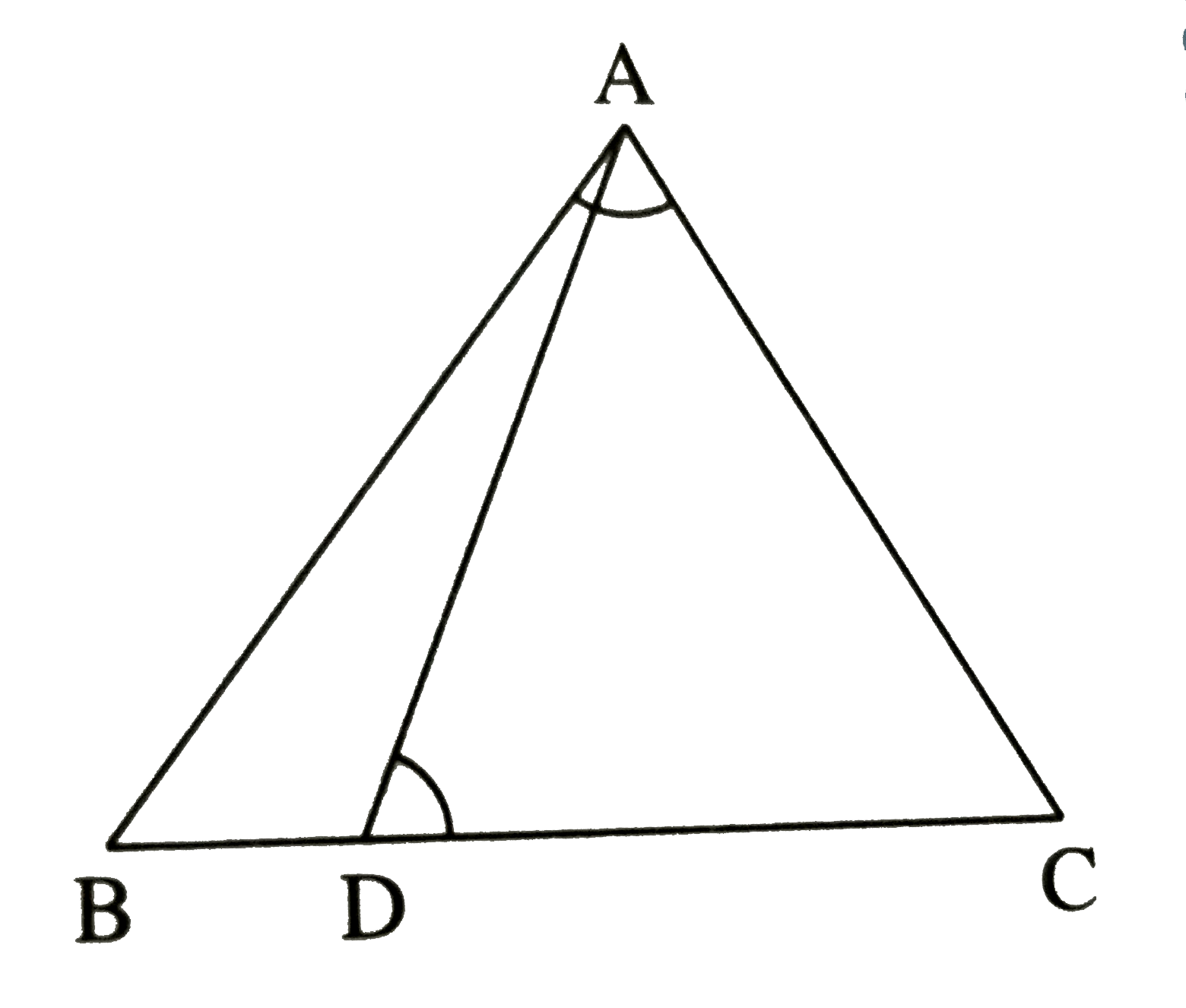
In the given figure , D is a point on the side BC of $\Delta ABC$ such that $\angle ADC=\angle BAC$. Prove that $C{A}^2=CB\times CD$.

Explanation

GIVEN `A Delta ABC` in which D is point on BC such that `angle ADC= angle BAC`.
TO PROVE `CA^(2)=CBxxCD`.
PROOF In `Delta ABC and Delta DAC`, we have
`angle BAC= angle ADC` (given)
`angle ACB= angle DCA` ( common)
`:. angle ABC~ Delta DAC` [ by AA-similarity]
So, the sides of `Delta ABC and Delta DAC` are proportional
`:. (CA)/(CB)=(CD)/(CA)`
Hence, `CA^(2)=CBxxCD`.