A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
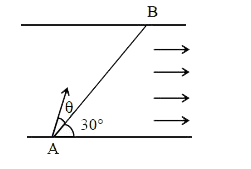
The correct Answer is:30
Step by step video, text & image solution for A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30^(@) with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle theta with the line AB should be _________ ""^(@), so that the swimmer reaches point B. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View Solution
Knowledge Check
A man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
A(u+vcosθ)dvsinθB(u−vcosθ)dvsinθC(u−vcosθ)dvcosθD(u+vcosθ)dvcosθA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river is 5 m/s. Swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be :
A10m/sB12m/sC5√5m/sD10√2m/sA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river water is 5ms. Swimmer takes 12 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
A10msB5msC5√5msD5√2ms
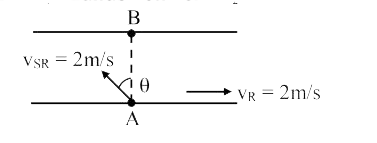
Find θ in the given situation so that the swimmer directly lands on the point B.
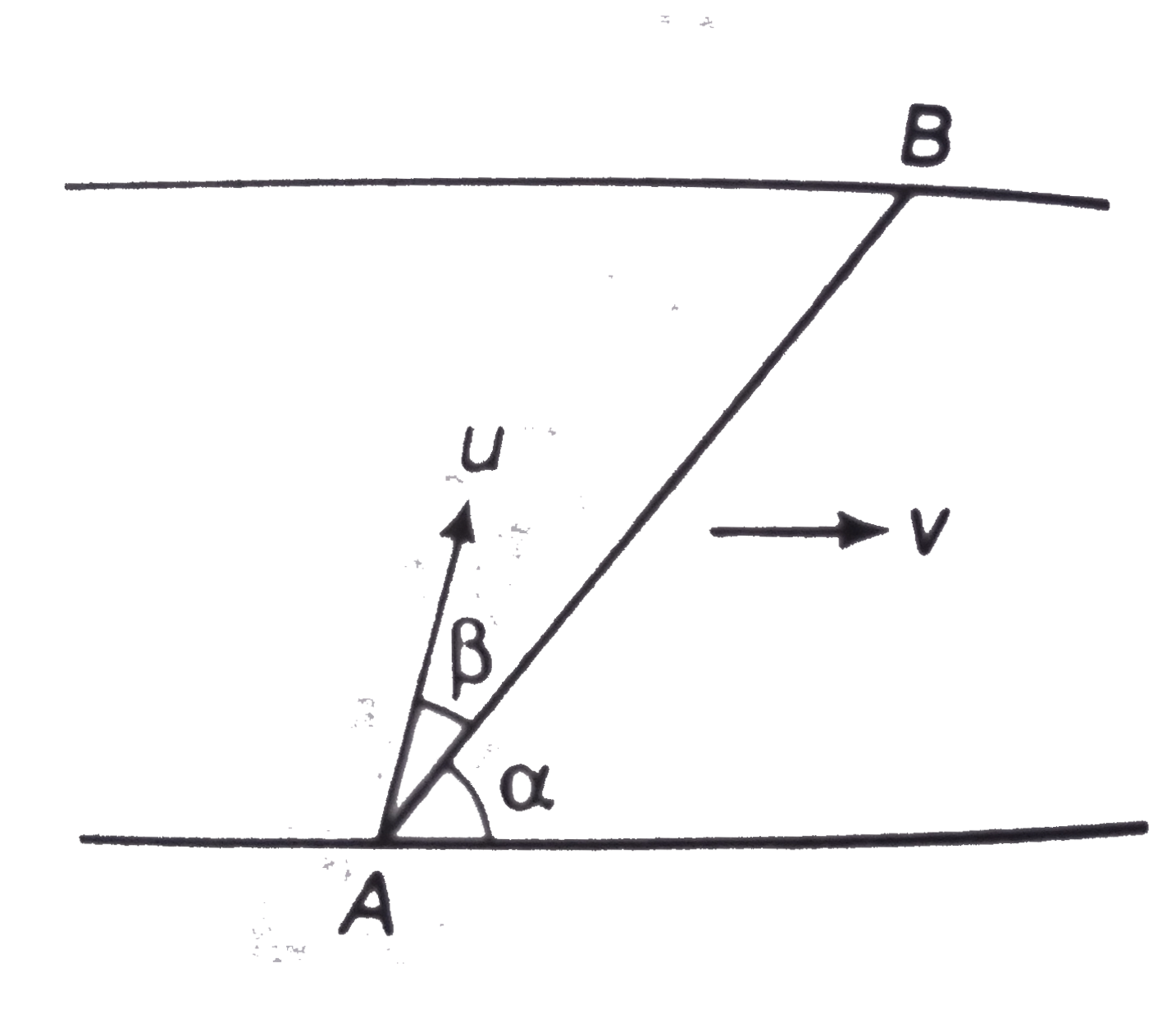
View SolutionA launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
View SolutionWidth of a river is 60m . A swimmer wants to cross the river such that he reaches from A to B directly. Point B is 45m ahead of line AC (perpendicular to river) Assume speed of river and speed of swimmer as equal. Swimmer must try to swim at angle θ with line AC .If the value of θ (in degrees) is N2 .Find N
View SolutionA swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
View SolutionTwo swimmers A and B start swimming from different positions on the same bank as shown in figure.The swimmer A swims at angle 90∘ with respect to the river to reach point P.He takes 120seconds to cross the river of width 10m.The swimmer B also takes the same time to reach the point P
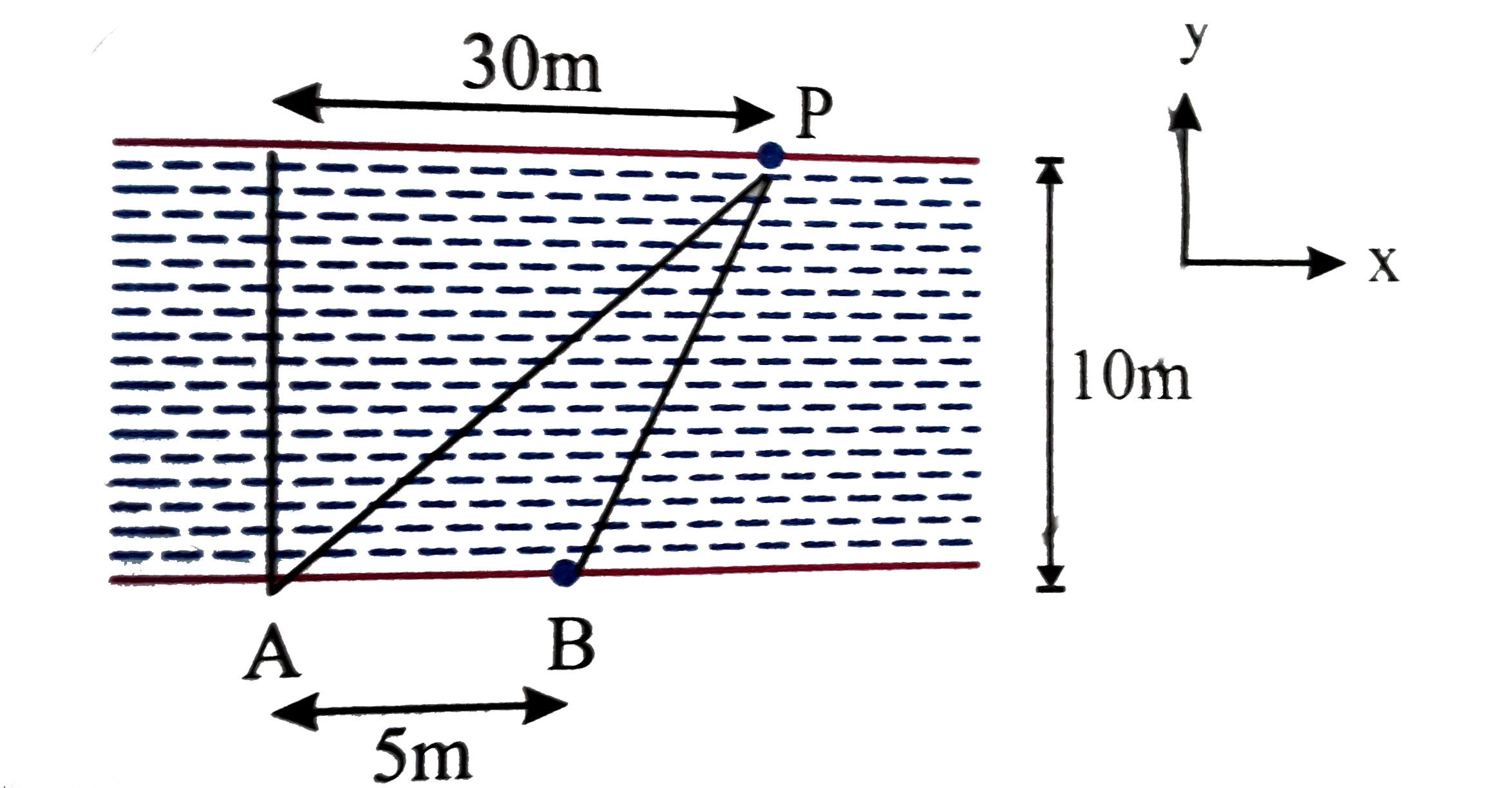
View Solution

