A swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river is 5 m/s. Swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be :
10m/s
12m/s
5√5m/s
10√2m/s
The correct Answer is:C
To find the velocity of the swimmer with respect to water, we can follow these steps:
Step 1: Identify the given information
- Width of the river (d) = 60 m
- Velocity of the river (Vw) = 5 m/s
- Time taken to cross the river (t) = 6 s
- Angle made with the direction of flow (θ) = 45°
Step 2: Calculate the swimmer's effective velocity across the river
The swimmer crosses the river in 6 seconds, so we can calculate the effective velocity (Vx) of the swimmer across the river:
Vx=dt=60m6s=10m/s
Step 3: Relate swimmer's velocity components
Since the swimmer makes an angle of 45° with the direction of the river flow, we can express the swimmer's velocity (Vs) in terms of its components:
- The horizontal component (Vx) and vertical component (Vy) of the swimmer's velocity are equal due to the angle of 45°.
- Therefore, we have:
Vx=Vcos(45°)
Vy=Vsin(45°)
Since cos(45°)=sin(45°)=1√2, we can say:
Vx=Vy=V√2
Step 4: Set up the equations
From Step 2, we know Vx=10m/s. Therefore:
V√2=10
V=10√2m/s
Step 5: Calculate the swimmer's velocity with respect to water
The swimmer's velocity with respect to water (Vs) can be expressed as:
Vs=Vx^i+Vy^j
Where:
- Vx=10m/s
- Vy=10m/s
Thus:
Vs=10^i+10^j
Step 6: Adjust for the river's velocity
The velocity of the river (Vw) is in the negative j direction:
Vw=5^j
The swimmer's velocity with respect to water is:
Vswimmer_water=Vs−Vw=(10^i+10^j)−(0^i+5^j)
Vswimmer_water=10^i+(10−5)^j=10^i+5^j
Step 7: Calculate the magnitude of the swimmer's velocity with respect to water
The magnitude of the swimmer's velocity with respect to water can be calculated using the Pythagorean theorem:
|Vswimmer_water|=√(10)2+(5)2
|Vswimmer_water|=√100+25=√125=5√5m/s
Final Answer
The velocity of the swimmer with respect to water is 5√5m/s.
---
- Width of the river (d) = 60 m
- Velocity of the river (Vw) = 5 m/s
- Time taken to cross the river (t) = 6 s
- Angle made with the direction of flow (θ) = 45°
The swimmer crosses the river in 6 seconds, so we can calculate the effective velocity (Vx) of the swimmer across the river:
Vx=dt=60m6s=10m/s
Since the swimmer makes an angle of 45° with the direction of the river flow, we can express the swimmer's velocity (Vs) in terms of its components:
- The horizontal component (Vx) and vertical component (Vy) of the swimmer's velocity are equal due to the angle of 45°.
- Therefore, we have:
Vx=Vcos(45°)
Vy=Vsin(45°)
Vx=Vy=V√2
From Step 2, we know Vx=10m/s. Therefore:
V√2=10
V=10√2m/s
The swimmer's velocity with respect to water (Vs) can be expressed as:
Vs=Vx^i+Vy^j
Where:
- Vx=10m/s
- Vy=10m/s
Vs=10^i+10^j
The velocity of the river (Vw) is in the negative j direction:
Vw=5^j
Vswimmer_water=Vs−Vw=(10^i+10^j)−(0^i+5^j)
Vswimmer_water=10^i+(10−5)^j=10^i+5^j
The magnitude of the swimmer's velocity with respect to water can be calculated using the Pythagorean theorem:
|Vswimmer_water|=√(10)2+(5)2
|Vswimmer_water|=√100+25=√125=5√5m/s
The velocity of the swimmer with respect to water is 5√5m/s.
Topper's Solved these Questions
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS
Explore 75 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)
Explore 26 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
Explore 6 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
- KINETIC THEORY OF GASES Book:MOTIONChapter:KINETIC THEORY OF GASES Exercise:EXERCISE-3 SECTION-B
Explore 16 Videos
Similar Questions
A bridge across the river makes an angle of 30∘ with the river bank. If the length of the bridge across the river is 60m, Find the width of the river.
View SolutionA steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?
View Solution
Knowledge Check
A swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river water is 5ms. Swimmer takes 12 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
A10msB5msC5√5msD5√2msTwo swimmers A and B start swimming from different positions on the same bank as shown in figure.The swimmer A swims at angle 90∘ with respect to the river to reach point P.He takes 120seconds to cross the river of width 10m.The swimmer B also takes the same time to reach the point P
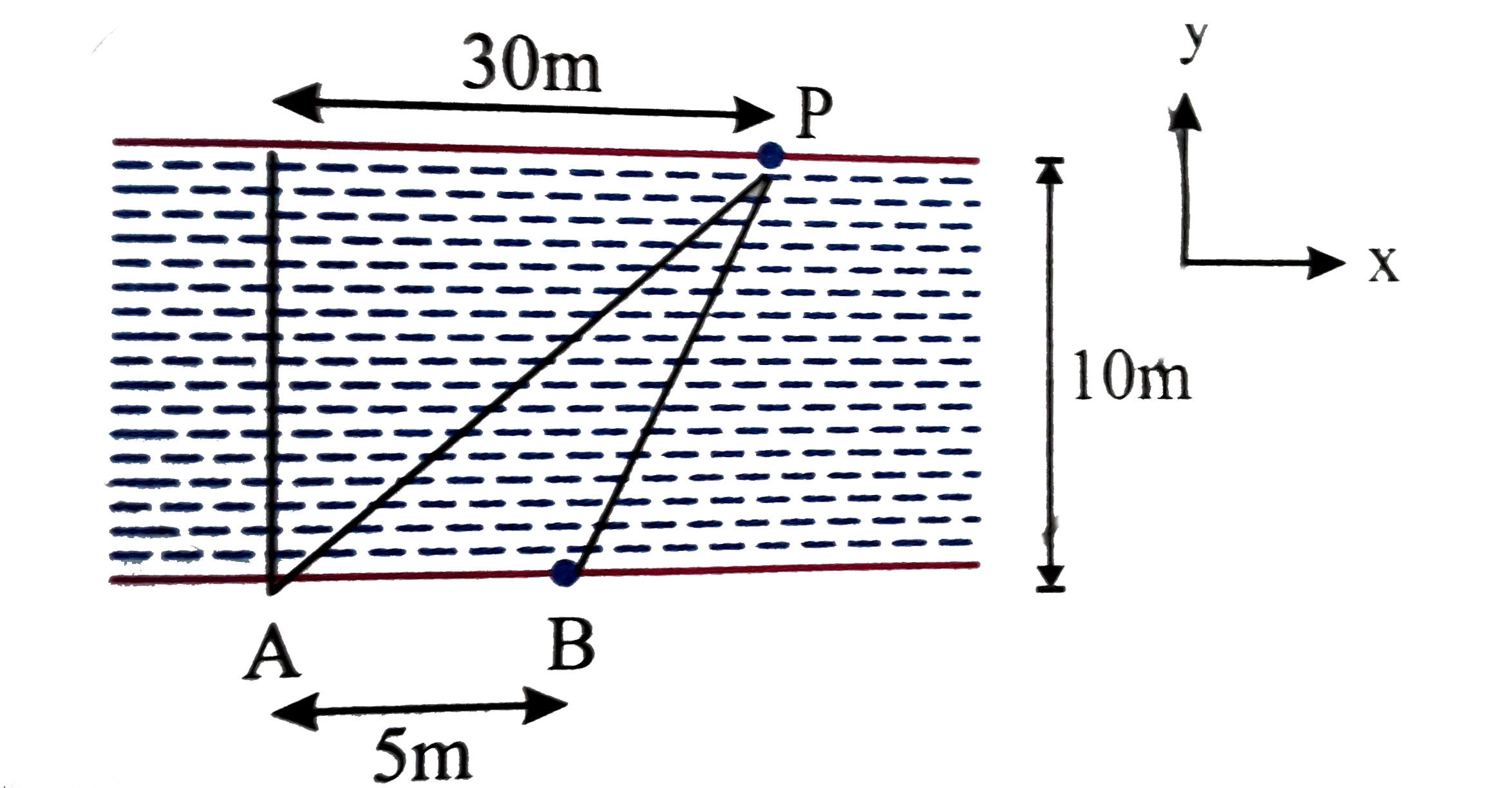 Avelocity of A with respect to river is 1/6m/sBriver flow velocity is 1/4m/sCVelocity of B along y-axis with respect to earth is 1/3m/s.DVelocity of B along x-axis with respect to earth is 5/24m/s.
Avelocity of A with respect to river is 1/6m/sBriver flow velocity is 1/4m/sCVelocity of B along y-axis with respect to earth is 1/3m/s.DVelocity of B along x-axis with respect to earth is 5/24m/s.A swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
A(2−√3)vB2(2−√3)vC4(2−√3)vD(2+√3)v
A bridge across a river makes an angles of 450 with the river bank as shown in Figure. If the lengthof the bridge across the river is 150m, what is the width of the river?
View SolutionVelocity of a swimmer with respect to a river is (ˆi+4ˆj)ms and velocity of the river flow is (2ˆj)ms then velocity of swimmer with respect to ground is (in m/s)
View SolutionTwo swimmers P and Q start swimming from different positions on the same bank as shown in the figure. The swimmer P swims at an angle 90∘ with respect to the river to reach point A. He takes 120 second to cross the river of width 10m. The swimmer Q also takes the same time to reach the point A. the velocity component of Q along x-axis with respect to ground is K/24. Find the value of K.

View SolutionA man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View SolutionA swimmer crosses a river with minimum possible time 10 Second. And when he reaches the other end starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in 15 sec. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume contant speed of river & swimmer)
View Solution

