A swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
(2−√3)v
2(2−√3)v
4(2−√3)v
(2+√3)v
To solve the problem, we need to analyze the swimmer's motion across the river while considering the river's current. Let's break it down step by step.
Step 1: Understand the Problem
The swimmer is crossing a river of width d while swimming at an angle of 120∘ with respect to the flow of the river, which has a velocity v. The swimmer experiences a drift of d2 downstream due to the river's current.
Step 2: Define the Components of Velocity
Let the speed of the swimmer with respect to the river be Vs. The swimmer's velocity can be broken down into two components:
- The component along the river flow (x-direction): Vscos(120∘)
- The component across the river (y-direction): Vssin(120∘)
Using trigonometric values:
- cos(120∘)=−12
- sin(120∘)=√32
Thus, we have:
- Vsx=Vscos(120∘)=−12Vs
- Vsy=Vssin(120∘)=√32Vs
Step 3: Analyze the Drift
The drift experienced by the swimmer while crossing the river is given as d2. The total time t taken to cross the river can be expressed in terms of the width d and the swimmer's y-component of velocity:
t=dVsy=d√32Vs=2d√3Vs
Step 4: Calculate the Drift Due to River Flow
During the time t, the river carries the swimmer downstream. The distance drifted downstream due to the river's current is:
Drift=v⋅t=v⋅2d√3Vs
Since the drift is given as d2, we can set up the equation:
v⋅2d√3Vs=d2
Step 5: Simplify the Equation
We can cancel d from both sides (assuming d≠0):
v⋅2√3Vs=12
Now, multiplying both sides by √3Vs:
2v=√32Vs
Rearranging gives:
Vs=4v√3
Step 6: Final Result
Thus, the speed of the swimmer with respect to the river is:
Vs=4v√3+2
The swimmer is crossing a river of width d while swimming at an angle of 120∘ with respect to the flow of the river, which has a velocity v. The swimmer experiences a drift of d2 downstream due to the river's current.
Let the speed of the swimmer with respect to the river be Vs. The swimmer's velocity can be broken down into two components:
- The component along the river flow (x-direction): Vscos(120∘)
- The component across the river (y-direction): Vssin(120∘)
- cos(120∘)=−12
- sin(120∘)=√32
- Vsx=Vscos(120∘)=−12Vs
- Vsy=Vssin(120∘)=√32Vs
The drift experienced by the swimmer while crossing the river is given as d2. The total time t taken to cross the river can be expressed in terms of the width d and the swimmer's y-component of velocity:
t=dVsy=d√32Vs=2d√3Vs
During the time t, the river carries the swimmer downstream. The distance drifted downstream due to the river's current is:
Drift=v⋅t=v⋅2d√3Vs
Since the drift is given as d2, we can set up the equation:
v⋅2d√3Vs=d2
We can cancel d from both sides (assuming d≠0):
v⋅2√3Vs=12
Now, multiplying both sides by √3Vs:
2v=√32Vs
Rearranging gives:
Vs=4v√3
Thus, the speed of the swimmer with respect to the river is:
Vs=4v√3+2
Similar Questions
A person is swimming with a speed of 10 m/s at an angle of 120° with the flow and reaches to a point directly opposite on the other side of the river. The speed of the flow is 'x m/s.
The value of 'x to the nearest integer is_________.
View SolutionThe velocity if a swimmer (v) in stil water is less than the velocity of water (u) in a river. Show that the swimmer must aim himself at an angles cos−1 (v/u) with upstream in order to cross the river along the shortest possible path. Find thr drifting (distance moved along the direction of stream in crossing the river) of the swimmer along this shortest possible path.
View Solution
Knowledge Check
A swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river is 5 m/s. Swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be :
A10m/sB12m/sC5√5m/sD10√2m/sA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The drift of the man along the direction of flow, when he arrives at the opposite bank is.A16√3kmB6√3cmC3√3kmD13√3kmA swimmer wishes to cross a river 500m width flowing at a rate u. his speed w.r.t. still water is v. for this he makes an angle θ with the vertical as shown in the given figure then:
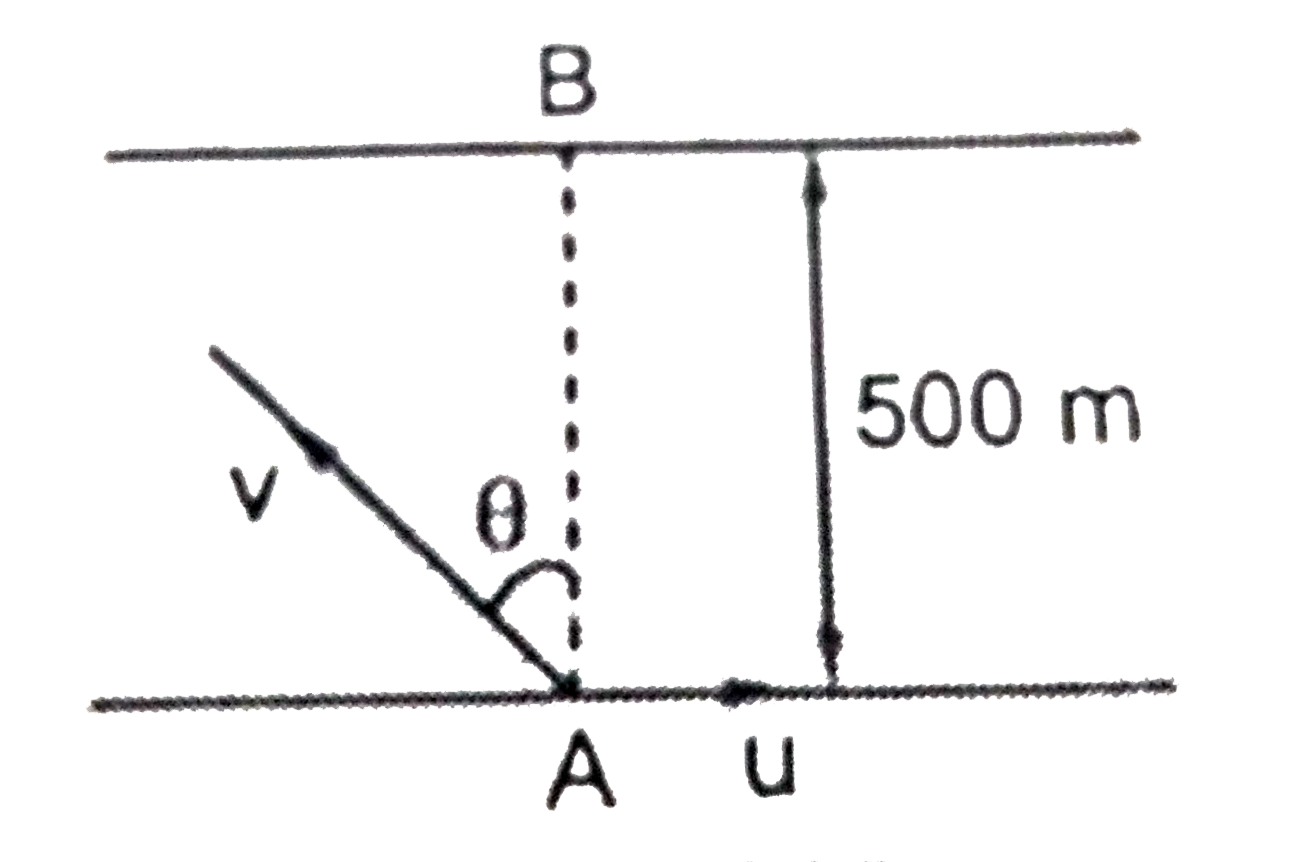 Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
A man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The time taken to cross the river is.
View SolutionA person, reaches a point directly opposite on the other bank of a flowing river, while swimming at a speed of 5 m/s at an angle of 120∘ with the flow. The speed of the flow must be
View SolutionA man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
View SolutionA swimmer crosses a river with minimum possible time 10 Second. And when he reaches the other end starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in 15 sec. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume contant speed of river & swimmer)
View SolutionA man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60° with the flow of direction while swimming, The time taken by him to cross the river will be
View Solution