In right-angled ΔABC,DandE trisect BC. Find the value of 8 (AEAC)2−5(ADAC)2
1
2
3
4
The correct Answer is:C
To solve the problem, we need to find the value of 8(AEAC)2−5(ADAC)2 in the right-angled triangle ΔABC where points D and E trisect BC.
1. Identify the Triangle and Trisection Points:
- Let BC be trisected by points D and E. This means BD=DE=EC.
- Let BD=DE=EC=x. Therefore, BC=3x.
2. Apply the Pythagorean Theorem:
- In triangle ABD:
AD2=AB2+BD2=AB2+x2(Equation 1)
- In triangle ABE:
AE2=AB2+BE2=AB2+(BD+DE)2=AB2+(2x)2=AB2+4x2(Equation 2)
- In triangle ABC:
AC2=AB2+BC2=AB2+(3x)2=AB2+9x2(Equation 3)
3. Express AEAC and ADAC:
- From Equations 2 and 3, we have:
AE2AC2=AB2+4x2AB2+9x2
- From Equations 1 and 3, we have:
AD2AC2=AB2+x2AB2+9x2
4. Substitute into the Expression:
- Substitute the expressions for AE2AC2 and AD2AC2 into the original expression:
8(AE2AC2)−5(AD2AC2)=8⋅AB2+4x2AB2+9x2−5⋅AB2+x2AB2+9x2
5. Combine the Terms:
- Combine the fractions:
=8(AB2+4x2)−5(AB2+x2)AB2+9x2
- Simplifying the numerator:
=8AB2+32x2−5AB2−5x2AB2+9x2=(8−5)AB2+(32−5)x2AB2+9x2
=3AB2+27x2AB2+9x2
6. Factor Out Common Terms:
- Factor out 3 from the numerator:
=3(AB2+9x2)AB2+9x2=3
Final Answer:
Thus, the value of 8(AEAC)2−5(ADAC)2 is 3.
- Let BC be trisected by points D and E. This means BD=DE=EC.
- Let BD=DE=EC=x. Therefore, BC=3x.
- In triangle ABD:
AD2=AB2+BD2=AB2+x2(Equation 1)
- In triangle ABE:
AE2=AB2+BE2=AB2+(BD+DE)2=AB2+(2x)2=AB2+4x2(Equation 2)
- In triangle ABC:
AC2=AB2+BC2=AB2+(3x)2=AB2+9x2(Equation 3)
- From Equations 2 and 3, we have:
AE2AC2=AB2+4x2AB2+9x2
- From Equations 1 and 3, we have:
AD2AC2=AB2+x2AB2+9x2
- Substitute the expressions for AE2AC2 and AD2AC2 into the original expression:
8(AE2AC2)−5(AD2AC2)=8⋅AB2+4x2AB2+9x2−5⋅AB2+x2AB2+9x2
- Combine the fractions:
=8(AB2+4x2)−5(AB2+x2)AB2+9x2
- Simplifying the numerator:
=8AB2+32x2−5AB2−5x2AB2+9x2=(8−5)AB2+(32−5)x2AB2+9x2
=3AB2+27x2AB2+9x2
- Factor out 3 from the numerator:
=3(AB2+9x2)AB2+9x2=3
Thus, the value of 8(AEAC)2−5(ADAC)2 is 3.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
In a ΔABC,AB=ACandAD⊥BC, then:
AAB<ADBAB>ADCAB=ADDAB≤ADIn a right angled ΔABC if ∠B=90∘,AC=2√5 and AB−BC=2 then what is the value of cos2A−cos2C ?
A35B45C√74D1√5
ABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
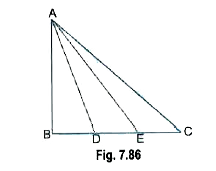
View SolutionIn Fig. 7.86, if D and E trisects BC. Prove that 8AE2=3AC2+5AD2.
View SolutionIn the figure AB=AC angle BAD=30∘andAE=AD, then the value of x is
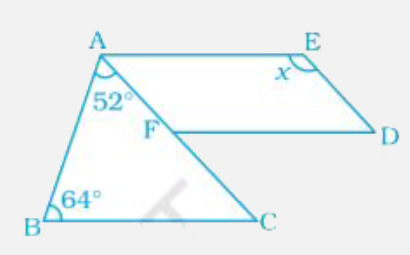
View SolutionIn the following figure, FD||BC||AE and AC||ED. Find the value of x.
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIn ΔABC, right angled at B, if AB=12cm, BC= x and AC=13cm, then the value of x is
View Solution