A square is inscribed in a quarter circle in such a manner that two of its adjacent vertices lie on two radli and are equidistant from the centre. The other two vertices lie on the circular arc. If the length of the side of the square is 20 cm, find the radius of the circle. (in cm.)
10√10
20√10
10√20
10√30
The correct Answer is:A
To solve the problem of finding the radius of the circle in which a square of side length 20 cm is inscribed in a quarter circle, we can follow these steps:
1. Understanding the Geometry:
- We have a quarter circle with a square inscribed in it. The square has two vertices on the radii of the quarter circle and the other two vertices on the arc of the quarter circle.
2. Labeling the Square:
- Let the side length of the square be s=20 cm.
- Label the center of the quarter circle as O, and the vertices of the square as A, B, C, and D such that A and B are on the radii and C and D are on the arc.
3. Finding the Diagonal of the Square:
- The diagonal AC of the square can be calculated using the formula for the diagonal of a square:
Diagonal=s√2=20√2 cm
4. Identifying the Radius:
- The radius of the quarter circle r can be expressed in terms of the diagonal of the square. The diagonal AC extends from the center O to point C on the arc. Therefore, the radius r is equal to the length of the diagonal:
r=20√2 cm
5. Calculating the Radius:
- To find the numerical value of the radius, we calculate:
r=20√2≈20×1.414≈28.28 cm
6. Final Result:
- The radius of the quarter circle is approximately 28.28 cm.
Final Answer:
The radius of the circle is 20√2 cm or approximately 28.28 cm.
- We have a quarter circle with a square inscribed in it. The square has two vertices on the radii of the quarter circle and the other two vertices on the arc of the quarter circle.
- Let the side length of the square be s=20 cm.
- Label the center of the quarter circle as O, and the vertices of the square as A, B, C, and D such that A and B are on the radii and C and D are on the arc.
- The diagonal AC of the square can be calculated using the formula for the diagonal of a square:
Diagonal=s√2=20√2 cm
- The radius of the quarter circle r can be expressed in terms of the diagonal of the square. The diagonal AC extends from the center O to point C on the arc. Therefore, the radius r is equal to the length of the diagonal:
r=20√2 cm
- To find the numerical value of the radius, we calculate:
r=20√2≈20×1.414≈28.28 cm
- The radius of the quarter circle is approximately 28.28 cm.
The radius of the circle is 20√2 cm or approximately 28.28 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A square is inscribed in a quarter-circle in such a manner that two of its adjacent vertices lie on the two radil at an equal distance from the centre, while the other two vertices lie on the circular arc. If the square has sides of length x, then the radius of the circle is
A√2xB16xπ+4C2x√πD√5x√2A square is inscribed in a quarter-circle in such a manner that two of its adjacent vertices lie on the two radii at an equal distance from the centre, while the other two vertices lie on the circular arc. If the square has sides of length x, then the radius of the circle is
A√2xB16xπ+4C2x√πDsqr(5)x√2A square is inscribed in a quarter circle in such a way that two of its adjacent vertices on the radius are equidistant from the centre and other two vertices lie on the circumference. If the side of square is √52 cm, then what is the radius (in cm) of the circle?
A2B2.5C5D10
In the figure ABCD is a square,whose vertices lie on the circle.Find the area of the shaded region,if the perimeter of the circle is 88 cm
View Solution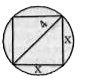
A square of side x is inscribed in a circle of radius 4 cm. Then x is
View SolutionThe side of a square is 10 cm. Find the area of circumscribed and inscribed circles.
View SolutionThe sum of circumferences of two circles is 132 cm. If the radius of one circles is 14 cm, find the radius of the other circle.
View SolutionA square is incribed in a quarter circle in such a way that two of its adjacent vertices on the radius are equidistant from the centre and other two vertices lie on the circumference. If the side of square is √52 cm, then what is the radius (in cm) of the circle ?
View Solution

