Question

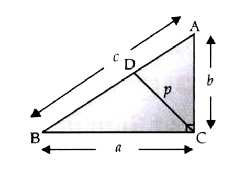
ABC is a right angled triangle in which $\angle C={90}^{\circ }$. If $BC=a,AB=c,CA=b$and the length of perpendicular from C to AB be p. then, $\frac{1}{a^2}+\frac{1}{b^2}=?$

Options

A. `1/p`
B. `2/(p^2)`
C. `1/(p^2)`
D. None of these

Answer

C

Explanation

To solve the problem step by step, we will use the properties of right-angled triangles and the relationship between the sides and the area.

1. Understand the Triangle: We have a right-angled triangle ABC where angle C is 90 degrees. The sides are defined as follows:
- BC = a (opposite to angle A)
- CA = b (opposite to angle B)
- AB = c (the hypotenuse)

2. Area of the Triangle: The area of triangle ABC can be calculated using the formula for the area of a triangle:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
If we take BC (a) as the base and CA (b) as the height, the area can be expressed as:
\( \text{Area} = \frac{1}{2} \times a \times b \)

3. Using the Perpendicular: The length of the perpendicular from point C to line AB is given as p. The area can also be expressed using this perpendicular:
\( \text{Area} = \frac{1}{2} \times c \times p \)
where c is the length of the hypotenuse AB.

4. Equating the Areas: Since both expressions represent the area of the same triangle, we can set them equal to each other:
\( \frac{1}{2} \times a \times b = \frac{1}{2} \times c \times p \)
Simplifying this gives:
\( a \times b = c \times p \)

5. Squaring the Equation: We will square both sides of the equation:
\( (a \times b)^2 = (c \times p)^2 \)
This expands to:
\( a^2 \times b^2 = c^2 \times p^2 \)

6. Using Pythagoras' Theorem: From the Pythagorean theorem, we know that:
\( c^2 = a^2 + b^2 \)
Substituting this into our equation gives:
\( a^2 \times b^2 = (a^2 + b^2) \times p^2 \)

7. Rearranging the Equation: Rearranging this equation, we can express it in terms of \( \frac{1}{a^2} + \frac{1}{b^2} \):
\( \frac{1}{a^2} + \frac{1}{b^2} = \frac{p^2}{a^2 \times b^2} \)

8. Final Expression: Therefore, we can conclude that:
\( \frac{1}{a^2} + \frac{1}{b^2} = \frac{p^2}{a^2 \times b^2} \)

Final Answer:
Thus, the value of \( \frac{1}{a^2} + \frac{1}{b^2} \) is \( \frac{p^2}{a^2 \times b^2} \).