An angle in a semicircle is
45∘
60∘
90∘
120∘
The correct Answer is:C
To solve the question "An angle in a semicircle is", we need to understand the properties of angles formed in a semicircle.
1. Understanding the Circle and Diameter:
- Draw a circle and label the endpoints of the diameter as points A and B.
- The line segment AB represents the diameter of the circle.
2. Identifying the Semicircle:
- The semicircle is the upper half of the circle that is formed when you draw the diameter AB.
- The points on the semicircle are all the points that lie on the circle above the line segment AB.
3. Drawing a Triangle:
- Choose any point C on the semicircle.
- Draw line segments AC and BC, forming triangle ABC.
4. Analyzing the Angle:
- The angle ACB is the angle formed at point C by the lines AC and BC.
- According to the properties of circles, specifically the inscribed angle theorem, the angle subtended by the diameter at any point on the semicircle is always a right angle.
5. Conclusion:
- Therefore, the angle ACB is 90 degrees.
Final Answer:
The angle in a semicircle is 90 degrees.
- Draw a circle and label the endpoints of the diameter as points A and B.
- The line segment AB represents the diameter of the circle.
- The semicircle is the upper half of the circle that is formed when you draw the diameter AB.
- The points on the semicircle are all the points that lie on the circle above the line segment AB.
- Choose any point C on the semicircle.
- Draw line segments AC and BC, forming triangle ABC.
- The angle ACB is the angle formed at point C by the lines AC and BC.
- According to the properties of circles, specifically the inscribed angle theorem, the angle subtended by the diameter at any point on the semicircle is always a right angle.
- Therefore, the angle ACB is 90 degrees.
The angle in a semicircle is 90 degrees.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)
Explore 22 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Consider the following statements :
1.The perpendicular bisector of chord of a circle does not pass through the centre of the circle.
2. The angle in a semicircle is a right angle.
Which of the statements given above is/are correct ?
View SolutionThe area of a semicircle is 308cm2. Find its perimeter
View Solution
Knowledge Check
Consider the following statements
I. The perpendicular bisector of a chord of a circle does not pass through the centre of the circle.
II. The angle in a semicircle is a right angle.
Which of the statements given above is/are correct?AOnly IBOnly IICBoth I and IIDNeither I nor IIThe angle in a semicircle measures
A180∘B60∘C90∘D36∘∠ACB is an angle in the semicircle of diameter AB =5 and AC : BC = 3 : 4 The area of the triangle ABC is
A6√2 sq. mB4 sq. cmC12 sq. cmD6 sq. cm
∠ACB is an angle in the semicircle of diameter AB = 5 and AC : BC = 3:4. The area of the triangle ABC is
View Solution∠ACB is an angle in the semicircle of diameter AB = 5 and AC : BC = 3:4. The area of the triangle ABC is
View SolutionThe figure below is made up of an isosceles triangle and a semicircle. Find the perimeter of the figure.
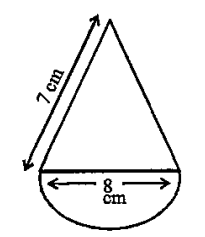
View SolutionThe area of a semicircle is 77cm2. Calculate its perimeter (in cm).
View SolutionThe area of a semicircle is 77cm2. Calculate its perimeter (in cm).
View Solution
