Question

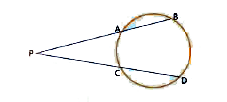
Two chords $AB\text{and}PQ$ of a circle intersect at D inside a circle. If AD = 4 cm., DB = 6 cm., QD = 3 cm., the length of PQ is equal to

Options

A. 11 cm
B. 8 cm
C. 9 cm.
D. 10 cm.

Answer

A

Explanation

To solve the problem, we will use the intersecting chords theorem, which states that if two chords intersect inside a circle, the products of the lengths of the segments of each chord are equal.

1. Identify the lengths of the segments:
- Given:
- \( AD = 4 \, \text{cm} \)
- \( DB = 6 \, \text{cm} \)
- \( QD = 3 \, \text{cm} \)
- We need to find the length of \( PQ \).

2. Use the intersecting chords theorem:
- According to the theorem:
\( AD \times DB = PD \times QD \)
- Substitute the known values:
\( 4 \times 6 = PD \times 3 \)

3. Calculate \( PD \):
- Calculate the left side:
\( 24 = PD \times 3 \)
- To find \( PD \), divide both sides by 3:
\( PD = \frac{24}{3} = 8 \, \text{cm} \)

4. Calculate the length of \( PQ \):
- The length of \( PQ \) is the sum of \( PD \) and \( QD \):
\( PQ = PD + QD \)
- Substitute the values:
\( PQ = 8 + 3 = 11 \, \text{cm} \)

5. Final Answer:
- The length of \( PQ \) is \( 11 \, \text{cm} \).

Summary:
The length of chord \( PQ \) is \( 11 \, \text{cm} \).