A square ABCD is inscribed in a circle of unit radius. Semicircles are described on each side as a diameter. The area of the region bounded by the four semicircles and the circle is
1 sq. unit
2 sq. unit
1.5 sq. unit
2.5 sq. unit
The correct Answer is:B
To solve the problem step by step, we need to find the area of the region bounded by the four semicircles and the circle.
Step 1: Understand the Configuration
We have a square ABCD inscribed in a circle with a unit radius. The semicircles are drawn on each side of the square as diameters.
Step 2: Find the Diameter of the Circle
Since the radius of the circle is 1 unit, the diameter D of the circle is:
D=2×radius=2×1=2 units
Step 3: Relate the Diameter to the Square
The diameter of the circle is equal to the diagonal of the square. Let s be the side length of the square. The diagonal d of the square can be expressed as:
d=s√2
Setting this equal to the diameter of the circle:
s√2=2
Solving for s:
s=2√2=√2 units
Step 4: Find the Radius of the Semicircles
The diameter of each semicircle is equal to the side of the square, which is s=√2. Therefore, the radius r of each semicircle is:
r=s2=√22 units
Step 5: Calculate the Area of One Semicircle
The area A of one semicircle is given by the formula:
A=12πr2
Substituting the radius:
A=12π(√22)2=12π(24)=12π(12)=π4 square units
Step 6: Calculate the Total Area of Four Semicircles
Since there are four semicircles:
Total Area of Semicircles=4×π4=π square units
Step 7: Calculate the Area of the Circle
The area of the circle with a radius of 1 unit is:
Area of Circle=πr2=π(1)2=π square units
Step 8: Calculate the Area of the Square
The area of the square with side length s=√2 is:
Area of Square=s2=(√2)2=2 square units
Step 9: Find the Area of the Shaded Region
The area of the region bounded by the semicircles and the circle is given by:
Area of Shaded Region=Total Area of Semicircles−(Area of Circle−Area of Square)
Substituting the values:
Area of Shaded Region=π−(π−2)=2 square units
Final Answer
Thus, the area of the region bounded by the four semicircles and the circle is:
2 square units
We have a square ABCD inscribed in a circle with a unit radius. The semicircles are drawn on each side of the square as diameters.
Since the radius of the circle is 1 unit, the diameter D of the circle is:
D=2×radius=2×1=2 units
The diameter of the circle is equal to the diagonal of the square. Let s be the side length of the square. The diagonal d of the square can be expressed as:
d=s√2
Setting this equal to the diameter of the circle:
s√2=2
Solving for s:
s=2√2=√2 units
The diameter of each semicircle is equal to the side of the square, which is s=√2. Therefore, the radius r of each semicircle is:
r=s2=√22 units
The area A of one semicircle is given by the formula:
A=12πr2
Substituting the radius:
A=12π(√22)2=12π(24)=12π(12)=π4 square units
Since there are four semicircles:
Total Area of Semicircles=4×π4=π square units
The area of the circle with a radius of 1 unit is:
Area of Circle=πr2=π(1)2=π square units
The area of the square with side length s=√2 is:
Area of Square=s2=(√2)2=2 square units
The area of the region bounded by the semicircles and the circle is given by:
Area of Shaded Region=Total Area of Semicircles−(Area of Circle−Area of Square)
Substituting the values:
Area of Shaded Region=π−(π−2)=2 square units
Thus, the area of the region bounded by the four semicircles and the circle is:
2 square units
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)
Explore 22 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
The area of the square inscribed in a circle of radius 8 cm is
A256 sq. cmB250 sq. cmC128sq. CmD125 sq. cmIf the four equal circles of radius 3 cm touch each other externally, then the area of the region bounded by the four circles is
A4(9−π) sq. cmB9(4−π) sq. cm.C5(6−π) sq. cm.D6(5−π) sq. cmA square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles isA4πR2(1−(12)n)B2πR2(1−(12)n)C3πR2(1−(13)n)DπR2(1−(12)n)
In the figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
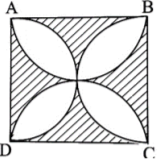
View SolutionABCD is a square of 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region. (π=3.14)
View SolutionThe square ABCD is inscribed in a circle of radius 1 unit. ABP is a straight line, PC is tangent to the circle. The length of PD is
View SolutionIn the given figure, ABCD is a square of side 14cm.Semicircles are drawn with each side of square as diameter. Find the area of the shaded region.
View SolutionIn the given figure, ABCD is a square of side 14 c m .Semicircles are drawn with each side of square as diameter. Find the area of the all region.
View Solution
