Question

The angle in a semi-circle is

Options

A. a) a reflex angle
B. b) an obtuse angle
C. c) an acute angle
D. d) a right angle

Answer

D

Explanation

To find the angle in a semicircle, we can follow these steps:

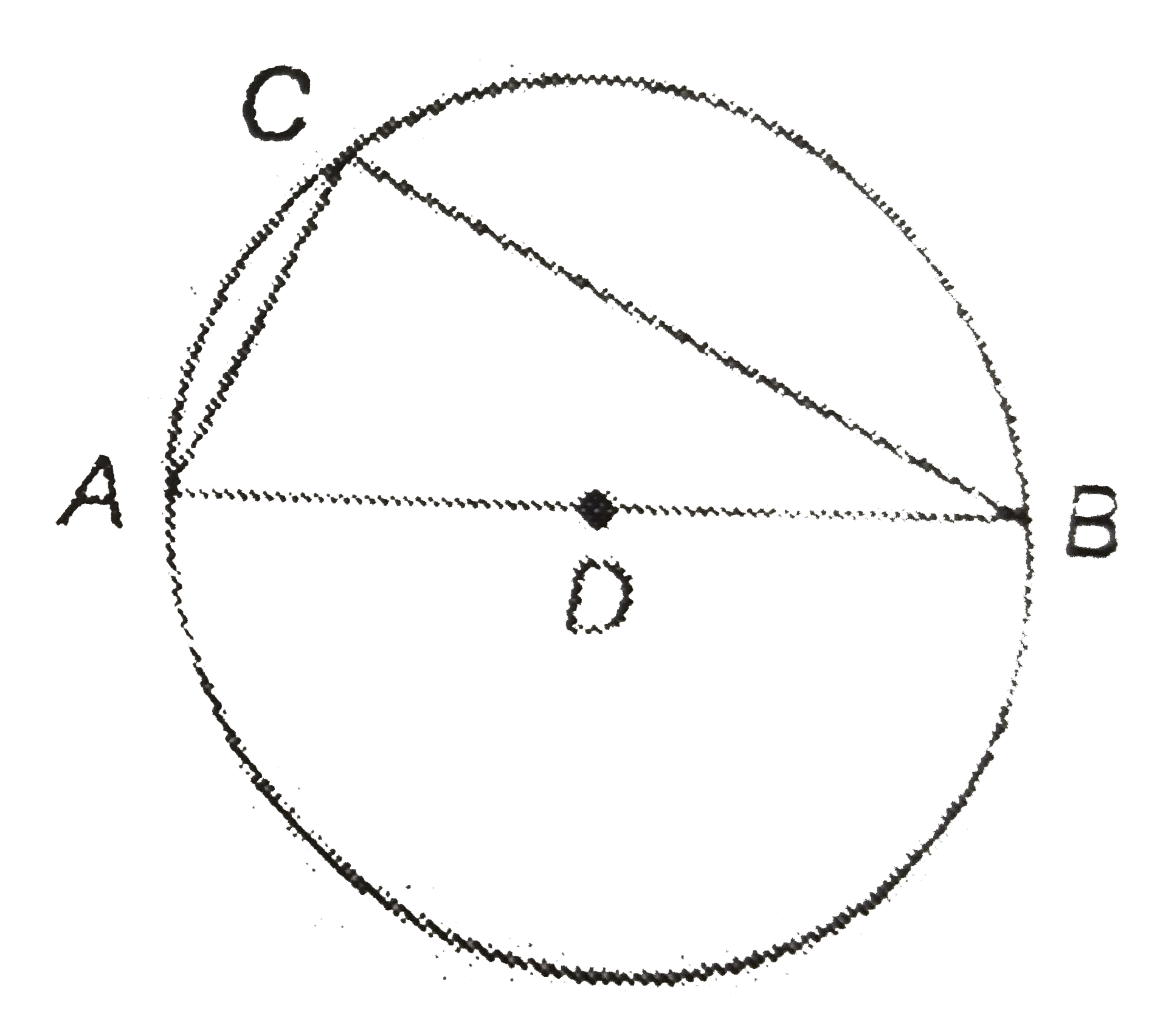
1. Draw a Circle: Start by drawing a circle with a diameter. Label the endpoints of the diameter as points A and B.

2. Identify the Center: Mark the center of the circle as point O, which is the midpoint of the diameter AB.

3. Draw a Triangle: Choose any point C on the circumference of the circle. This point will help us form triangle ABC, where AB is the diameter.

4. Understand the Angles: According to the properties of circles, the angle subtended by the diameter at any point on the circle (in this case, angle ACB) is always a right angle (90 degrees).

5. Apply the Angle Property: We know that the angle subtended at the center (angle AOB) is twice the angle subtended at the circumference (angle ACB). Since AB is a straight line, angle AOB is 180 degrees.

6. Calculate the Angle: Using the property mentioned, we can express the relationship as:
\( \text{Angle ACB} = \frac{\text{Angle AOB}}{2} = \frac{180^\circ}{2} = 90^\circ \)

7. Conclusion: Therefore, the angle in a semicircle (angle ACB) is 90 degrees.

Final Answer:
The angle in a semicircle is 90 degrees (a right angle).

---