In an isosceles triangle DEF,∠D=110∘. If I is the in centre of the triangle, then what is the value (in degrees) of ∠EIF?
110
130
145
155
The correct Answer is:C
To find the value of angle ∠EIF in the isosceles triangle DEF where ∠D=110∘, we can follow these steps:
Step 1: Understand the properties of the triangle
In an isosceles triangle, two sides are equal, and the angles opposite those sides are also equal. Here, since D is the vertex angle, the base angles E and F are equal.
Step 2: Set up the equation for the angles
The sum of the angles in any triangle is 180∘. Therefore, we can set up the equation:
∠D+∠E+∠F=180∘
Substituting the known value:
110∘+∠E+∠F=180∘
Since ∠E=∠F, we can denote ∠E=∠F=x:
110∘+2x=180∘
Step 3: Solve for x
Rearranging the equation gives:
2x=180∘−110∘
2x=70∘
x=35∘
Thus, ∠E=∠F=35∘.
Step 4: Determine the angles at the incenter
The incenter I of a triangle is the point where the angle bisectors of the triangle intersect. The angles ∠E and ∠F are bisected by the lines from I to E and I to F, respectively.
Since ∠E=35∘, the angle at I from E is:
∠EID=35∘2=17.5∘
Similarly, for ∠F:
∠FID=35∘2=17.5∘
Step 5: Calculate ∠EIF
In triangle EIF:
∠EIF+∠EID+∠FID=180∘
Substituting the known values:
∠EIF+17.5∘+17.5∘=180∘
∠EIF+35∘=180∘
∠EIF=180∘−35∘=145∘
Final Answer
Thus, the value of ∠EIF is 145∘.
---
In an isosceles triangle, two sides are equal, and the angles opposite those sides are also equal. Here, since D is the vertex angle, the base angles E and F are equal.
The sum of the angles in any triangle is 180∘. Therefore, we can set up the equation:
∠D+∠E+∠F=180∘
Substituting the known value:
110∘+∠E+∠F=180∘
Since ∠E=∠F, we can denote ∠E=∠F=x:
110∘+2x=180∘
Rearranging the equation gives:
2x=180∘−110∘
2x=70∘
x=35∘
Thus, ∠E=∠F=35∘.
The incenter I of a triangle is the point where the angle bisectors of the triangle intersect. The angles ∠E and ∠F are bisected by the lines from I to E and I to F, respectively.
∠EID=35∘2=17.5∘
Similarly, for ∠F:
∠FID=35∘2=17.5∘
In triangle EIF:
∠EIF+∠EID+∠FID=180∘
Substituting the known values:
∠EIF+17.5∘+17.5∘=180∘
∠EIF+35∘=180∘
∠EIF=180∘−35∘=145∘
Thus, the value of ∠EIF is 145∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)
Explore 109 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
Explore 35 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
In an isosceles triangle DEF,∠D=110∘. If I is the in centre of the triangle, then what is the value (in degrees) of ∠EIF?
A110B130C145D155In an isosceles triangle PQR, ∠P=130∘. If I is the in-centre of the triangle, what is the value (in degrees) of ∠QIR?
A130B120C155D165In the given figure, ABCD is a rhombos and BCE is an isosceles triangle, with BC = CE, ∠CBE=84∘ and ∠ADC=78∘. What is the value (in degree) of ∠DEC ?
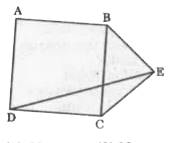 A1) 20B2) 28C3) 33D4) 36
A1) 20B2) 28C3) 33D4) 36
In a ΔABC,AD is the bisector of the angle A meeting BC at D. If I is the in centre of the triangle, then AI:DI is equal to
View SolutionThe vertical angle of an isosceles triangle is 110∘ . What is value of product of the digits in the measure of one of the equal angles?
View SolutionIn an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is 1000 (b) 1200 (c) 1100 (d) 1300
View SolutionIf △ABC≅△DEF then
View SolutionDEF is an isosceles triangle with such that DE = DF = 60 cm and EF = 96 cm. DG is a median to base EF. What is the length (in cm) of DG?
View Solution