Question

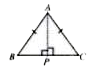
ABC is an isosceles triangle such that $AB=AC$and $AD$is the median to the base $BC$with $\angle ABC={35}^{\circ }$ . Then $\angle BAD$ is

Options

A. `35^@`
B. `55^@`
C. `70^@`
D. `110^@`

Answer

B

Explanation

To find the angle $$\angle BAD$$ in the isosceles triangle $$ABC$$ where $$AB=AC$$, $$AD$$ is the median to the base $$BC$$, and $$\angle ABC={35}^{\circ }$$, we can follow these steps:

1. Identify the Angles in Triangle ABC:
Since \( ABC \) is an isosceles triangle with \( AB = AC \), the angles opposite these sides will also be equal. Thus, \( \angle ABC = \angle ACB = 35^\circ \).

2. Calculate Angle A:
The sum of the angles in a triangle is always \( 180^\circ \). Therefore, we can calculate \( \angle A \) as follows:
\( \angle A + \angle ABC + \angle ACB = 180^\circ \)
Substituting the known values:
\( \angle A + 35^\circ + 35^\circ = 180^\circ \)
\( \angle A + 70^\circ = 180^\circ \)
\( \angle A = 180^\circ - 70^\circ = 110^\circ \)

3. Understanding the Median AD:
Since \( AD \) is the median to the base \( BC \), it divides \( \triangle ABC \) into two smaller triangles, \( ABD \) and \( ACD \), which are congruent. This means that \( \angle BAD = \angle CAD \).

4. Using the Properties of Angles:
In triangle \( ABD \), we know:
\( \angle BAD + \angle ABD + \angle ADB = 180^\circ \)
Since \( AD \) is the median, \( \angle ADB = 90^\circ \) (as the median to the base in an isosceles triangle creates two right triangles).

5. Substituting Known Values:
Let \( \angle BAD = x \). Thus, we have:
\( x + 35^\circ + 90^\circ = 180^\circ \)
Simplifying this gives:
\( x + 125^\circ = 180^\circ \)
\( x = 180^\circ - 125^\circ = 55^\circ \)

6. Conclusion:
Therefore, \( \angle BAD = 55^\circ \).

Final Answer:
\( \angle BAD = 55^\circ \)