PQR is an equilateral triangle. MN is drawn parallel to QR such that M is on PQ and N is on PR. If PN = 6 cm, then the length of MN is
3 cm
6 cm
12 cm
4.5 cm
The correct Answer is:B
To solve the problem, we will use the properties of similar triangles.
1. Identify the Triangle: We have an equilateral triangle PQR. This means all sides are equal, and all angles are 60 degrees.
2. Draw the Triangle: Let's draw triangle PQR with points P, Q, and R. Mark the points M on PQ and N on PR such that MN is parallel to QR.
3. Understand the Parallel Lines: Since MN is parallel to QR, triangles PMN and PQR are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the ratios of corresponding sides of these triangles are equal.
4. Set Up the Ratio: Let the length of MN be x. Since MN is parallel to QR, we can set up the following ratio:
PNPR=MNQR
Given that PN = 6 cm, and since PQR is equilateral, PR = QR.
5. Express PR and QR: Let the length of each side of the equilateral triangle PQR be 's'. Therefore, PR = QR = s.
6. Substitute Known Values: Substitute the known values into the ratio:
6s=xs
7. Solve for x: Since the sides PR and QR are equal, we can simplify the equation:
6=x
Therefore, the length of MN is 6 cm.
Final Answer:
The length of MN is 6 cm.
---
PNPR=MNQR
Given that PN = 6 cm, and since PQR is equilateral, PR = QR.
6s=xs
6=x
Therefore, the length of MN is 6 cm.
The length of MN is 6 cm.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)
Explore 109 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
The centroid of an equilateral triangle ΔPQR is L. If PQ = 18 cm, then the length of PL is :
A4√3cmB6√3cmC3√3cmD5√3cmIn ΔPQR, If ∠R=∠P, QR=4 cm and PR = 5 cm. Then, the length of PQ is
A4 cmB5 cmC2 cmD2.5 cmPQRS is a parallclogram such that PQ is parallel to SR and SP is parallel to RQ. The length of side PQ is 20 cm. M is point between P and Q such that the length of PM is 3 cm. N is a points between points S and R. Find the length of SN such that segment MN divides the parallelogram in two regions with equal areas.
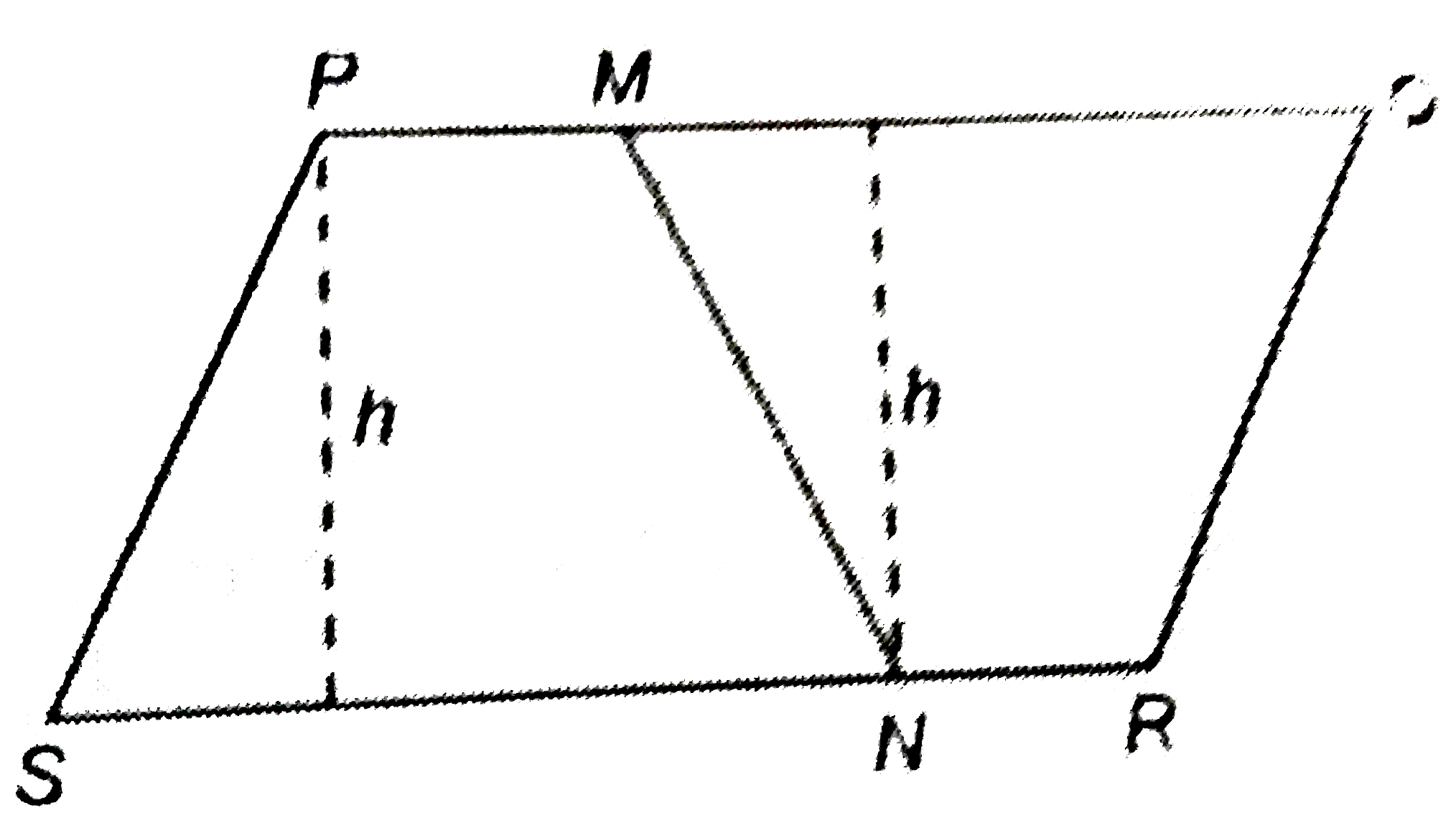 A15B17C16D18
A15B17C16D18

The length of the straight line PQR is 22 cm. If PQ : QR m = 4: 7, find the length of PQ.
View SolutionLet PQRS be a parallelogram whose diagonals PR and QS intersect at O. If triangle QRS is an equilateral triangle having a side of length 10 cm, then what is the length of the diagonal PR?
View SolutionPQR is a rigid equilateral triangle frame of a side length L. Forces F1,F2 and F3 are acting along PQ,QR,PR. If the system is in rotational equilibrium find the relation between the forces.
View SolutionIn ΔPQR, ∠PQR=90∘, PQ=6 and QR=8 then the length of seg PR is……. .

View SolutionIn ΔPQR, QR=10, RP=11 and PQ=12. D is the midpoint of PR, DE is drawn parallel to PQ meeting QR in E. EF is drawn parallel to RP meeting PQ in F. What is the length of DF?
View Solution

