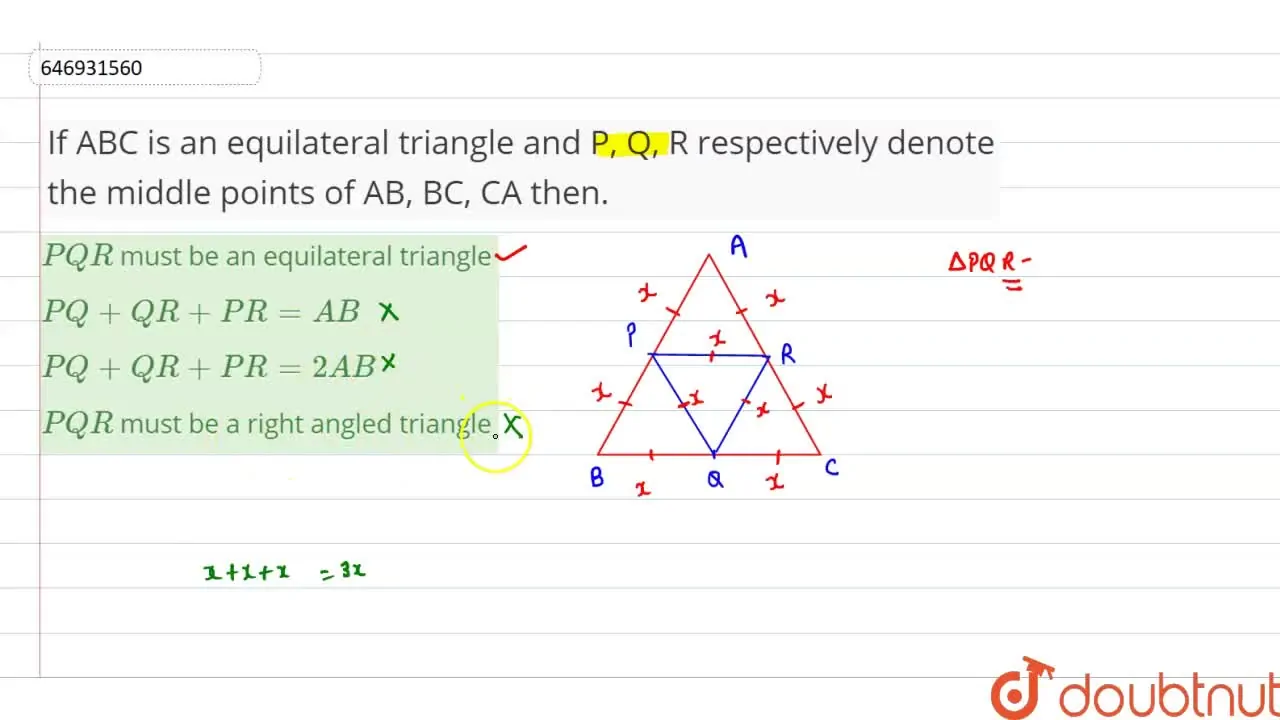
If ABC is an equilateral triangle and P, Q, R respectively denote the middle points of AB, BC, CA then.

A

$P Q R$ must be an equilateral triangle

B

$P Q + Q R + P R = A B$

C

$P Q + Q R + P R = 2 A B$

D

$P Q R$ must be a right angled triangle

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to analyze the properties of triangle ABC and the midpoints P, Q, and R.
1. Draw Triangle ABC:
- Start by sketching an equilateral triangle ABC where all sides are equal. Let the length of each side be denoted as $A B = B C = C A = x$ .
2. Identify Midpoints:
- Mark the midpoints of each side:
- Let $P$ be the midpoint of side $A B$ .
- Let $Q$ be the midpoint of side $B C$ .
- Let $R$ be the midpoint of side $C A$ .
3. Determine Lengths of Segments:
- Since $P$ , $Q$ , and $R$ are midpoints:
- The length of $A P = P B = \frac{x}{2}$
- The length of $B Q = Q C = \frac{x}{2}$
- The length of $C R = R A = \frac{x}{2}$
4. Calculate Lengths of PQ, QR, and PR:
- To find the lengths of segments $P Q$ , $Q R$ , and $P R$ , we can use the properties of midpoints in a triangle:
- The segment $P Q$ connects the midpoints of sides $A B$ and $B C$ .
- By the midpoint theorem, $P Q$ is parallel to $A C$ and half its length, so $P Q = \frac{1}{2} \times A C = \frac{x}{2}$ .
- Similarly, $Q R = \frac{1}{2} \times A B = \frac{x}{2}$ and $P R = \frac{1}{2} \times B C = \frac{x}{2}$ .
5. Sum of Lengths:
- Now, calculate the total length of $P Q + Q R + P R$ :
$P Q + Q R + P R = \frac{x}{2} + \frac{x}{2} + \frac{x}{2} = \frac{3 x}{2}$
6. Comparison with AB:
- Since $A B = x$ , we can compare:
$P Q + Q R + P R = \frac{3 x}{2} \neq A B$
7. Conclusion:
- Since $P Q R$ consists of segments that are equal in length and each side is half the length of the corresponding side of triangle ABC, triangle $P Q R$ is also equilateral.
- Therefore, the correct conclusion is that triangle $P Q R$ is an equilateral triangle.
Final Answer:
The correct option is that $P Q R$ must be an equilateral triangle.

Updated on:7/8/2024

|

Class 14 MATHS GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

If ABC is an equilateral triangle and P, Q, R respectively denote the middle points of AB, BC, CA then.
APQR must be an equilateral triangle
B $P Q + Q R + P R = A B$
C $P Q + Q R + P R = 2 A B$
DPQR must be a right angled triangle
ABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of $△ P Q R$ is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
A $4 \sqrt{3} c m^{2}$
B $8 \sqrt{3} c m^{2}$
C $\sqrt{3} / 3 c m^{2}$
D $\sqrt{3} / 4 c m^{2}$
$Δ A B C$ is an equilateral triangle, AB = 6. The points P, Q and Rare midpoints of AB, BC and CA respectively. The perimeter of PBCR is
A18
B15
C9
D12

KIRAN PUBLICATION-GEOMETRY-TRY YOURSELF

Home
Ask Doubt
Profile