The side QR of an equilateral triangle PQR is produced to the point S in such a way that QR = RS and P is joined to S. Then the measure of ∠PSR is
30∘
15∘
60∘
45∘
The correct Answer is:A
To find the measure of angle ∠PSR in the given problem, we will follow these steps:
Step 1: Draw the Equilateral Triangle
First, we need to draw an equilateral triangle PQR. In an equilateral triangle, all sides are equal and all angles are 60∘.
Step 2: Extend Side QR to Point S
Next, extend the side QR to a point S such that QR=RS. This means that the length of RS is equal to the length of QR.
Step 3: Identify the Angles
Since PQR is an equilateral triangle, we know:
- ∠PQR=60∘
- ∠QRP=60∘
- ∠RPQ=60∘
Step 4: Use the External Angle Theorem
According to the external angle theorem, the measure of an external angle (in this case, ∠PSR) is equal to the sum of the measures of the two opposite internal angles. Here, the internal angles are ∠PQR and ∠QRP.
Step 5: Calculate ∠PSR
Since ∠PSR is the external angle at point S:
∠PSR=∠PQR+∠QRP
Substituting the values:
∠PSR=60∘+60∘=120∘
Step 6: Conclusion
Thus, the measure of ∠PSR is 120∘.
---
First, we need to draw an equilateral triangle PQR. In an equilateral triangle, all sides are equal and all angles are 60∘.
Next, extend the side QR to a point S such that QR=RS. This means that the length of RS is equal to the length of QR.
Since PQR is an equilateral triangle, we know:
- ∠PQR=60∘
- ∠QRP=60∘
- ∠RPQ=60∘
According to the external angle theorem, the measure of an external angle (in this case, ∠PSR) is equal to the sum of the measures of the two opposite internal angles. Here, the internal angles are ∠PQR and ∠QRP.
Since ∠PSR is the external angle at point S:
∠PSR=∠PQR+∠QRP
Substituting the values:
∠PSR=60∘+60∘=120∘
Thus, the measure of ∠PSR is 120∘.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)109videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
The base QR of an equilateral triangle PQR lies on X-axis. The co-ordinates of the point Q are (-4,0) and origin is the mid-point of the base. Find the co-ordinates of the points P and R.
View SolutionThe base QR of an equilateral triangle PQR lies on x-axis. The coordinates of the point Q are (-4, 0) and origin is the midpoint of the base. Find the coordinates of the points P and R.
View Solution
Knowledge Check
- Question 1 - Select One
PQR is an equilateral triangle. MN is drawn parallel to QR such that M is on PQ and N is on PR. If PN = 6 cm, then the length of MN is
A3 cmB6 cmC12 cmD4.5 cm - Question 2 - Select One
The base QR of an equilateral triangle PQR lies on x-axis. The coordinates of the point Q are (−4,0) and origin is the midpoint of the base. Find the coordinates of the points P and R.
AP(0,5√4)orP(0,−5√4)andR(3,2)BP(0,4√3)orP(0,−4√3)andR(4,0)CP(0,3√2)orP(0,−3√2)andR(3,1)DP(0,2√5)orP(0,−2√5)andR(3,5)
1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
View SolutionIn Fig. 6.1, side QR of a ΔPQR has been produced to the point S. If ∠PRS=115°and∠P=45°,then ∠Q is equal to,
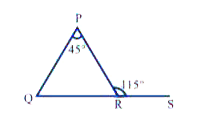 View Solution
View SolutionThe vertex P of an equilateral triangle △PQR is at (2,3) and the equation of the opposite side QR is given by x+y=2. Find the possible equations of the side PQ.
View SolutionIn the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2
 View Solution
View SolutionS is the incentre of △PQR . If ∠PSR=125∘, then the measure of ∠PQR is:
View SolutionA straight line through the vertex P of a triangle PQR intersects the side QR at the point S and the circuecirele of the triangle PQR at the point T. If S is not the centre of the circumeircle, then
View Solution
