A, B and C are batsmen. The ratio of the runs scored by them in a certain match are given below : A:B=5:3 and B:C=4:5. In all they scored 564 runs. The number of runs scored by B is:
124
104
114
144
The correct Answer is:D
To solve the problem step by step, we will first express the runs scored by A, B, and C in terms of a common variable based on the given ratios.
Step 1: Understand the Ratios
The ratios provided are:
- A : B = 5 : 3
- B : C = 4 : 5
Step 2: Express Runs in Terms of a Common Variable
Let's denote the runs scored by A, B, and C as follows:
- Let the runs scored by B be 3x (from the ratio A:B = 5:3).
- Then, the runs scored by A will be 5x.
- From the second ratio B:C = 4:5, we can express C in terms of B:
- If B = 4y, then C = 5y.
Since B is common in both ratios, we need to equate the two expressions for B:
- 3x=4y
Step 3: Solve for x and y
From the equation 3x=4y, we can express y in terms of x:
- y=3x4
Now substitute y back into the expression for C:
- C = 5y=5(3x4)=15x4
Step 4: Total Runs Scored
Now we can express the total runs scored by A, B, and C:
- Total runs = A + B + C
- Total runs = 5x+3x+15x4
To add these, we need a common denominator:
- Convert 5x and 3x to have a denominator of 4:
- 5x=20x4
- 3x=12x4
Now we can add:
- Total runs = 20x4+12x4+15x4=47x4
Step 5: Set Up the Equation
According to the problem, the total runs scored by A, B, and C is 564:
- 47x4=564
Step 6: Solve for x
Multiply both sides by 4 to eliminate the fraction:
- 47x=564×4
- 47x=2256
Now divide by 47:
- x=225647=48
Step 7: Calculate Runs Scored by B
Now that we have the value of x, we can find the runs scored by B:
- B = 3x=3×48=144
Final Answer
The number of runs scored by B is 144.
The ratios provided are:
- A : B = 5 : 3
- B : C = 4 : 5
Let's denote the runs scored by A, B, and C as follows:
- Let the runs scored by B be 3x (from the ratio A:B = 5:3).
- Then, the runs scored by A will be 5x.
- From the second ratio B:C = 4:5, we can express C in terms of B:
- If B = 4y, then C = 5y.
Since B is common in both ratios, we need to equate the two expressions for B:
- 3x=4y
From the equation 3x=4y, we can express y in terms of x:
- y=3x4
- C = 5y=5(3x4)=15x4
Now we can express the total runs scored by A, B, and C:
- Total runs = A + B + C
- Total runs = 5x+3x+15x4
- Convert 5x and 3x to have a denominator of 4:
- 5x=20x4
- 3x=12x4
- Total runs = 20x4+12x4+15x4=47x4
According to the problem, the total runs scored by A, B, and C is 564:
- 47x4=564
Multiply both sides by 4 to eliminate the fraction:
- 47x=564×4
- 47x=2256
- x=225647=48
Now that we have the value of x, we can find the runs scored by B:
- B = 3x=3×48=144
The number of runs scored by B is 144.
Topper's Solved these Questions
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-IV
30 Videos
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-V
64 Videos
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-II
49 Videos
- PROFIT AND LOSS BOOK - KIRAN PUBLICATIONCHAPTER - PROFIT AND LOSS EXERCISE - TEST YOURSELF
23 Videos
- SEQUENCE AND SERIES BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TEST YOURSELF
20 Videos
Similar Questions
In an innings of a cricket match three players, A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2 the number of runs scored by A was 161 b. 171 c. 181 d. 185
View SolutionRuns scored by Girish in a match are 10 more than the balls faced by Vishal. The number of balls faced by Girish is 5 more than the number of runs scored by Vishal. Together they have scored 50 runs and Girish has faced 15 balls less than that faced by Vishal. What is the numberof runs scored by Girish?
View Solution
Knowledge Check
What is the average run scored by the batsman man in the five matches?
AA.50BB.49CC.45DD.46.25In an innings of a cricket match, three players A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2, the number of runs scored by A was
A171B181C185D161In a cricket match the total number of runs scored by Sachin, Vinod and Sourav is 285. The ratio of the number of runs scored by Sachin and Sourav is 3:2 and that of the runs scored by Sourav and Vinod is also 3:2. The number of runs scored by Sachin In that match Is
A135B90C60D140
The given pie chart shows runs scored by A in 6 matches

In the given pie chart what is the average runs scored in all matches
View SolutionThe table given below shows the runs scored by 4 different batsmen B1, B2, B3 and B4 in 5 different matches of a series.
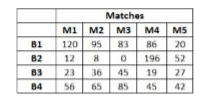
What is the per match average numberof run scored by batsman B3?
View SolutionThe table given below shows the runs scored by 4 different batsmen B1, B2, B3 and B4 in 5 different matches of a series.
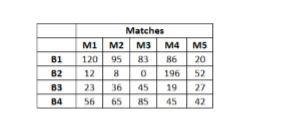
What is the difference in the total numberof runs scored by B1 and B4 in these 5 matches?
View SolutionThe table given below shows the runs scored by 4 different batsmen B1, B2, B3 and B4 in 5 different matches of a series.
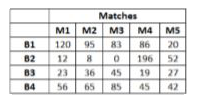
What is the per batsman average runs scored by these batsmen in M5?
View SolutionTotal runs scored by three batsmen x, y and z are 1584. Ratio of runs scored by x and y is 4 : 3 and y and z is 5 : 3. How many runs are scored by x?
View Solution
