In a cricket match the total number of runs scored by Sachin, Vinod and Sourav is 285. The ratio of the number of runs scored by Sachin and Sourav is 3:2 and that of the runs scored by Sourav and Vinod is also 3:2. The number of runs scored by Sachin In that match Is
135
90
60
140
The correct Answer is:A
To solve the problem step by step, we can follow these instructions:
Step 1: Define the Variables
Let the number of runs scored by Sachin be S, by Sourav be R, and by Vinod be V.
Step 2: Set Up the Ratios
From the problem, we know:
- The ratio of runs scored by Sachin to Sourav is S:R=3:2.
- The ratio of runs scored by Sourav to Vinod is R:V=3:2.
Step 3: Express Runs in Terms of a Common Variable
Using the ratios, we can express the runs in terms of a common variable:
- Let R=2x (where x is a common multiplier).
- Then, from the first ratio S:R=3:2, we have S=32R=32(2x)=3x.
- From the second ratio R:V=3:2, we have V=23R=23(2x)=43x.
Step 4: Write the Total Runs Equation
According to the problem, the total runs scored by Sachin, Sourav, and Vinod is 285:
S+R+V=285
Substituting the expressions we found:
3x+2x+43x=285
Step 5: Combine the Terms
To combine the terms, we need a common denominator. The common denominator for the terms is 3:
9x3+6x3+4x3=285
Combining the fractions:
19x3=285
Step 6: Solve for x
To find x, multiply both sides by 3:
19x=285×3
Calculating the right side:
19x=855
Now, divide by 19:
x=85519=45
Step 7: Find the Runs Scored by Sachin
Now that we have x, we can find the number of runs scored by Sachin:
S=3x=3×45=135
Final Answer
Thus, the number of runs scored by Sachin in that match is 135.
---
Let the number of runs scored by Sachin be S, by Sourav be R, and by Vinod be V.
From the problem, we know:
- The ratio of runs scored by Sachin to Sourav is S:R=3:2.
- The ratio of runs scored by Sourav to Vinod is R:V=3:2.
Using the ratios, we can express the runs in terms of a common variable:
- Let R=2x (where x is a common multiplier).
- Then, from the first ratio S:R=3:2, we have S=32R=32(2x)=3x.
- From the second ratio R:V=3:2, we have V=23R=23(2x)=43x.
According to the problem, the total runs scored by Sachin, Sourav, and Vinod is 285:
S+R+V=285
Substituting the expressions we found:
3x+2x+43x=285
To combine the terms, we need a common denominator. The common denominator for the terms is 3:
9x3+6x3+4x3=285
Combining the fractions:
19x3=285
To find x, multiply both sides by 3:
19x=285×3
Calculating the right side:
19x=855
Now, divide by 19:
x=85519=45
Now that we have x, we can find the number of runs scored by Sachin:
S=3x=3×45=135
Thus, the number of runs scored by Sachin in that match is 135.
Topper's Solved these Questions
- RATIO AND PROPORTION Book:KIRAN PUBLICATIONChapter:RATIO AND PROPORTION Exercise:TEST YOURSELF
Explore 19 Videos
- RATIO AND PROPORTION Book:KIRAN PUBLICATIONChapter:RATIO AND PROPORTION Exercise:TYPE-VIII
Explore 5 Videos
- PROFIT AND LOSS Book:KIRAN PUBLICATIONChapter:PROFIT AND LOSS Exercise:TEST YOURSELF
Explore 23 Videos
- SEQUENCE AND SERIES Book:KIRAN PUBLICATIONChapter:SEQUENCE AND SERIES Exercise:TEST YOURSELF
Explore 20 Videos
Similar Questions
In an innings of a cricket match three players, A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2 the number of runs scored by A was 161 b. 171 c. 181 d. 185
View SolutionThe line chart given below represents the runs scored by Kohli and Sharma against 5 teams.
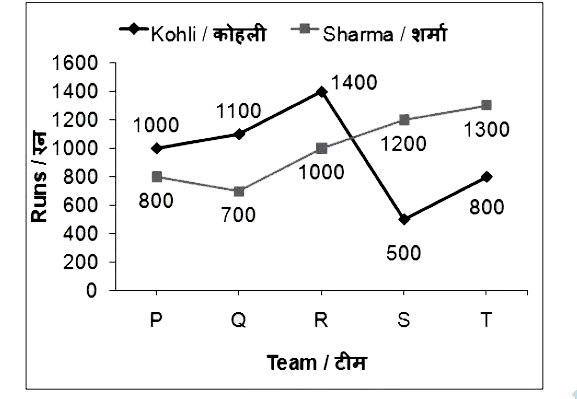
Total runs scored by Sharma against 5 teams is what percent of total runs scored by Kohli against 5 teams?
View Solution
Knowledge Check
In an innings of a cricket match, three players A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2, the number of runs scored by A was
A171B181C185D161Total runs scored by three batsmen x, y and z are 1584. Ratio of runs scored by x and y is 4 : 3 and y and z is 5 : 3. How many runs are scored by x?
A742B614C516D720If x runs are scored by A y runs by B and z runs by C, then x:y=y:z=3:2. If total number of runs scored by A, B and C is 342, the runs scored by each would be respectively
A144, 96, 64B162, 108, 72C180, 120, 80D189, 126, 84
The table given below show the runs scored by 5 players in four matches .
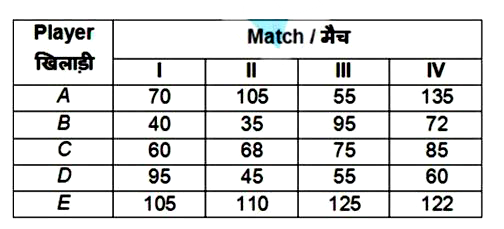
Runs scored by C in match II is how much percent more than the runs scored by C in match I?
View SolutionThe table given below shows the runs scored by 5 players in four matches .
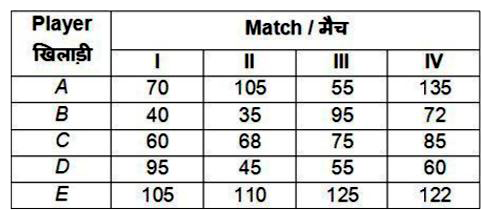
What is the difference between total runs scored by A and B in four matches?
View SolutionThe line chart given below represents the runs scored by Kohli and Sharma against 5 teams.
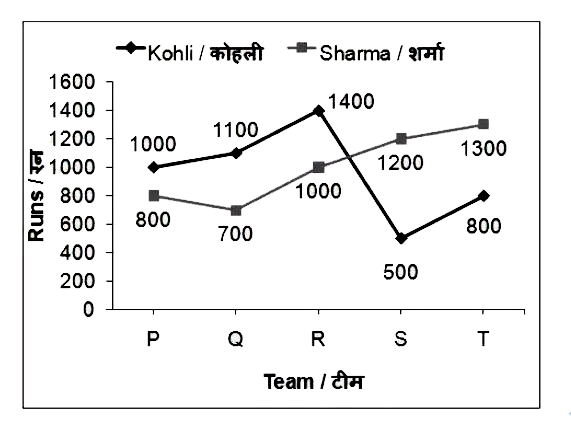
What is the total runs scored by Kohli against 5 teams?
View SolutionThe table given below shows the runs scored by 5 players in four matches .
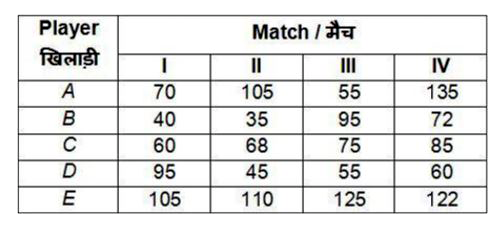
Runs scored by A in match II is what percent of the total runs scored by these five players in match II?
View SolutionA, B and C are batsmen. The ratio of the runs scored by them in a certain match are given below : A:B=5:3 and B:C=4:5. In all they scored 564 runs. The number of runs scored by B is:
View Solution
