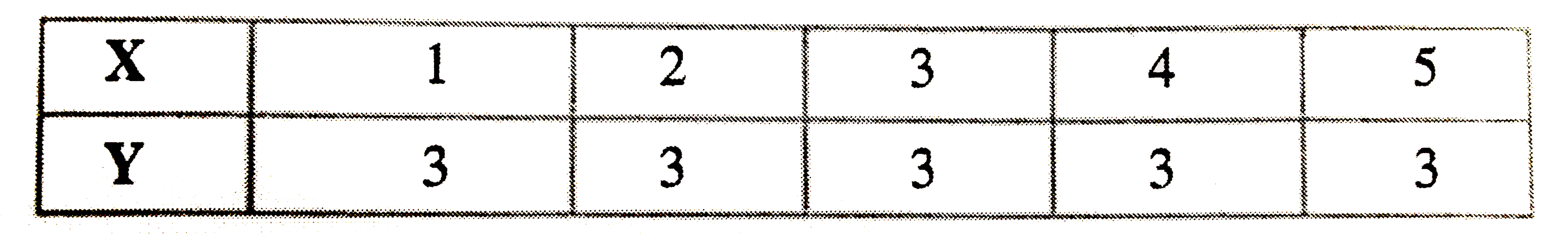If the coefficient of correlation between x and y os 0.6, covariance is 27 and variance of y is 25, then what is the variance x?
9/5
81/25
9
81
The correct Answer is:D
To find the variance of x given the coefficient of correlation, covariance, and variance of y, we can use the following relationship:
rxy=Cov(x,y)√Var(x)⋅Var(y)
Where:
- rxy is the coefficient of correlation between x and y,
- Cov(x,y) is the covariance between x and y,
- Var(x) is the variance of x,
- Var(y) is the variance of y.
Given:
- rxy=0.6
- Cov(x,y)=27
- Var(y)=25
We need to find Var(x).
Step 1: Substitute the known values into the formula
Substituting the known values into the correlation formula:
0.6=27√Var(x)⋅25
Step 2: Rearrange the equation
To isolate √Var(x), we can multiply both sides by √Var(x)⋅25:
0.6⋅√Var(x)⋅25=27
Next, divide both sides by 0.6:
√Var(x)⋅25=270.6
Calculating the right side:
270.6=45
So we have:
√Var(x)⋅25=45
Step 3: Square both sides
Now, square both sides to eliminate the square root:
Var(x)⋅25=452
Calculating 452:
452=2025
So we have:
Var(x)⋅25=2025
Step 4: Solve for Var(x)
Now, divide both sides by 25 to find Var(x):
Var(x)=202525
Calculating the division:
Var(x)=81
Final Answer
Thus, the variance of x is:
Var(x)=81
- rxy is the coefficient of correlation between x and y,
- Cov(x,y) is the covariance between x and y,
- Var(x) is the variance of x,
- Var(y) is the variance of y.
- rxy=0.6
- Cov(x,y)=27
- Var(y)=25
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the correlation coefficient between x and y is 0.6, covariance is 27 and variance of y is 25, then what is the variance of x?
A95B8125C9D81If the covariance between x and y is 30, variance of x is 25 and variance of y is 144, then what is the correlation coefficient?
A0.4B0.5C0.6D0.7If the covariance between x and y is 30. variance of A is 25 and variance of y is 144, then what is the correlation coefficient?
A0.4B0.5C0.6D0.7
Calculate coefficient of correlation between series X and Y.

View SolutionThe coefficient of correlation between X and Y is 0.6. Their covariance is 4.8 var (x)=9. Find the value of σy.
View SolutionCoefficient of correlation between two variable X and Y is 0.32. Their covariance is 7.86. The variance of X is 10. Find the standard deviation of Y-series.
View SolutionFind the Kari Pearson's Coefficient of correlation between x and y for the data

View SolutionThe coefficient of correlation between random variables X and Y is 0.28, covariance between X and Y is 7.6 and the variance of X is 9, then the standard deviation of Y series is
View Solution